菲克定律是指在不依靠宏观的混合作用发生的传质现象时，描述分子扩散过程中传质通量与浓度梯度之间关系的定律。菲克定律是阿道夫·菲克（Adolf Fick）于1855年提出。由菲克第二定律可以得到动态扩散的偏微分方程。求解可以得到浓度分布和流出曲线。不确定这个问题有没有解析解，不过数值求解是一种较为通用的解决方法。fipy是目前难得的还活着的PDE求解python包，作者根据官方示例改写本程序。工具/原料morepython27(必须)fipy(必须)spyder(建议)注意本文的发稿时间，2018年3月方法/步骤1/13分步阅读

安装fipy会有一定的难度，不在本篇范围，建议去官网查看，截至发稿，fipy还是建议在python27下使用

2/13

理解需要求解的问题

一个一维动态传质问题。在x轴上一段范围内。起初所有地方的浓度均为0。右侧端点处的浓度为1。然后溶质自由扩散。

由菲克第二定律的微分方程可以模拟这个过程。我们希望在合理的精度和时间范围内数值模拟这个过程。

3/13

再次给出链接，有python程序和运行的录屏

1oWWc-PZGfo0m2Un6-C3vSg

4/13

先给出全部程序的截图

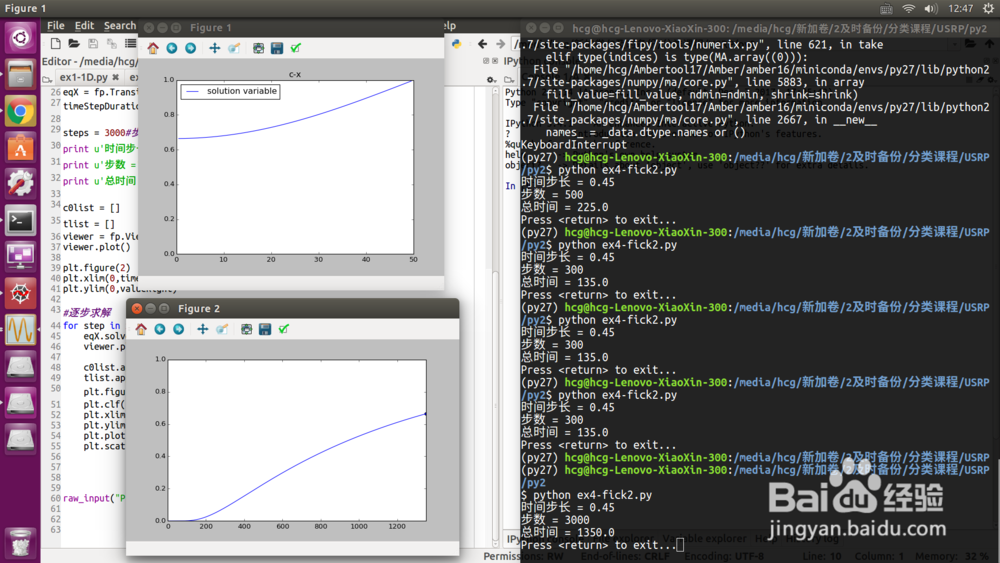
5/13

展示一下最终的运行结果，有这两张图，figure1是浓度随位置的曲线，figure2是流出曲线。这是Ubuntu下的运行截图，win10也可以运行，链接视频里面就是在win10运行的。

6/13

首先导入需要使用的包。本文使用fipy求解偏微分方程。

FiPy是一种基于标准有限体积法（finite volume methodFVM）的面向对象的偏微分方程（PDE）求解器，用Python编写。 该框架由美国国家标准与技术研究院（NIST）材料测量实验室（MML）的材料科学与工程部（MSED）和理论与计算材料科学中心（CTCMS）开发。

是目前为数不多的还活跃的开源PDEpython求解工具包

这是它的官网www.ctcms.nist.gov/fipy/

2017年1月还出过更新，期待继续发展。

fipy程序在win下有一些BUG，很是麻烦，如果非要使用，建议尝试Linux

7/13

然后设定求解区域，或者说离散化求解区域。这里离散化为50个点。

初始化为0

8/13

D为扩散系数，即菲克定律中的D扩散系数

然后设立边界条件，右侧为定值，及最右端的点的浓度为1

左侧不设定，fipy默认设定为狄利克雷边界

9/13

然后设立微分方程，fipy有其独特的面向对象的微分方程表达方式，此处ExplicitDiffusionTerm表示二阶梯度，TransientTerm表示随时间的一阶偏导。

10/13

然后设立步数和时间步长。此问题稳定的时间步长小于这个值（dx**2 / (2 * D)）取其0.9。也可以自信尝试增大此值。

步数step建议一开始测试的时候小一些，比如300.然后确定程序无误以后开一波3000步的模拟看看。

11/13

为流出曲线简历list来存储，c0list存放x=0处的浓度，tlist存放时间，以便于最后画出流出曲线。

然后建立绘图区，给浓度曲线（浓度关于x的曲线，随时间变化）绘图

12/13

原先最为困难的地方，方程求解，此时却最为简单，fipy有封装好的求解器可以求解，然而win版却时常碰到BUG。几行代码，循环求解，win版后台由scipy进行求解。

13/13

等时间走完了，就绘制流出曲线，即x=0处的浓度随时间的变化。

可以适当增加step（步数）来看看最后会怎样

注意事项

python的缩进

建议在cmd (anaconda prompt) 里面运行，可以看到动态连续变化的图片

PYTHONFIPY偏微分方程PDE菲克定律