MATLAB的空间曲面功能包括空间网格图，空间网面图，三角形空间网格图和等高线图等功能。工具/原料moreMATLAB软件方法/步骤1/6分步阅读

空间网格图

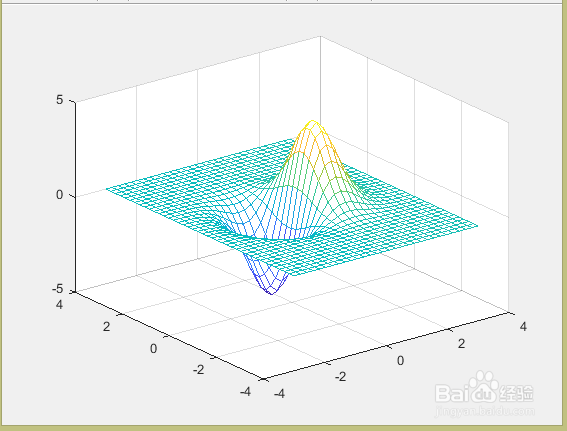
mesh(X,Y,Z)%根据行数列数相等的二维数组X,Y,Z绘制空间网格图。meah指令主要用于绘制二元函数的曲面图形。

=meshgrid(x,y)%根据以为数组x和y生成二维网格数据数组X和Y

如：

y=linspace(-4,4,40);

x=linspace(-3,3,30);

y=linspace(-4,4,40);

=meshgrid(x,y);;

Z=10*X.*exp(-X.^2-Y.^2);

mesh(X,Y,Z)

2/6

空间网格图

surf%根据行数列数相等的二维数组X,Y,Z绘制空间网格图

如：

x=linspace(-2,2,30);

y=linspace(-3,3,40);

=meshgrid(x,y);

Z=X.^2+Y.^2;

surf(X,Y,Z)

3/6

三角形空间网格图

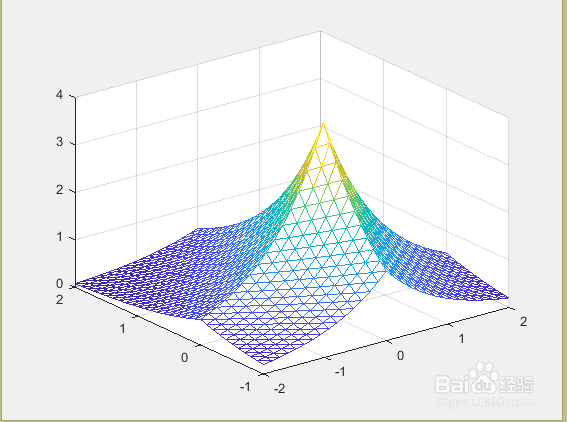
trimesh(tri,X,Y,Z)%根据数组X,Y,Z和三角形网数组tri绘制三角形空间网格图。

tri=delaunay(X,Y)%根据数组X和Y生成三角形网数组

如：

Z=4*exp(a+b);tri=delaunay(X,Y);

x=linspace(-2,2,31);

y=linspace(-1,2,31);

=meshgrid(x,y);

a=-abs(X);

b=-abs(Y);

Z=4*exp(a+b);

tri=delaunay(X,Y);

trimesh(tri,X,Y,Z)

4/6

三角形空间网格图

trisurf(tri,X,Y,Z)%根据数组X,Y,Z和三角形网数组tri绘制三角形空间网格图。

tri=delaunay(X,Y)%根据数组X和Y生成三角形网数组

如：

Z=4*exp(a+b);tri=delaunay(X,Y);

x=linspace(-2,2,31);

y=linspace(-1,2,31);

=meshgrid(x,y);

a=-abs(X);

b=-abs(Y);

Z=4*exp(a+b);

tri=delaunay(X,Y);

trisurf(tri,X,Y,Z)

5/6

等高线图

=contour3(x,y,z,n)%根据x,y,z绘制n条三维等高线。返回等高线组和句柄值

clabel(C,h)%根据等高线组C和等高线值

cabel(C,h,manual)%手动标注等高线值

如：

x=linspace(-pi,pi,40);

y=linspace(-pi,pi,40);

=meshgrid(x,y);

Z=X.^2+Y.^2;

=contour3(X,Y,Z,5);

clabel(C,h,manual);

6/6

带等高线的空间网格线

meshc(X,Y,Z)%根据数组X,Y,Z绘制带等高线的空间网格图

如：

x=linspace(-pi,pi,40);

y=linspace(-pi,pi,40);

=meshgrid(x,y);

Z=X.^2+Y.^2;

meshc(X,Y,Z)