假定一个工作日为8小时，时间以分钟为单位。利用MATLAB软件模拟一个工作日内完成服务的个数及顾客平均等待时间t。工具/原料more电脑MATLAB软件单服务员的排队模型1/1分步阅读

某商店有一个售货员，顾客陆续来到，售货员逐个地接待顾客．当到来的顾客较多时，一部分顾客便须排队等待，被接待后的顾客便离开商店．设：

1．顾客到来间隔时间服从参数为0.1的指数分布．

２．对顾客的服务时间服从［４，１５］上的均匀分布．

３．排队按先到先服务规则，队长无限制．

系统的假设：1/3

顾客源是无穷的；

2/3

排队的长度没有限制；

3/3

到达系统的顾客按先后顺序依次进入服务， 即“先到先服务”。

符号说明 1/1

w：总等待时间；

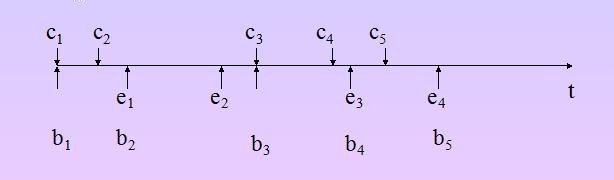
ci：第i个顾客的到达时刻；

bi：第i个顾客开始服务时刻；

ei：第i个顾客服务结束时刻．

xi：第i-1个顾客与第i个顾客之间到达的间隔时间；

yi：对第i个顾客的服务时间。

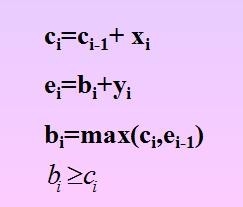方法/步骤41/11

初始化：令i=1，ei-1=0，w=0

2/11

产生间隔时间随机数xi~参数为0.1的指数分布

ci=xi , bi=xi

3/11

产生服务时间随机数yi~的均匀分布

ei=bi+yi

4/11

累计等待时间：w=w+bi-c

5/11

准备下一次服务：i=i+1

6/11

产生间隔时间随机数xi~参数为0.1的指数分布

ci=ci-1+ xi

7/11

确定开始服务时间：bi=max(ci,ei-1)

若bi＞480，则继续往下；若bi=480,则返回步骤3。

8/11

i=i-1,t=w/i。

输出结果：完成服务个数：m=i

平均等待时间：t

9/11

按上述1-8步骤做出模型框图，如图所示。

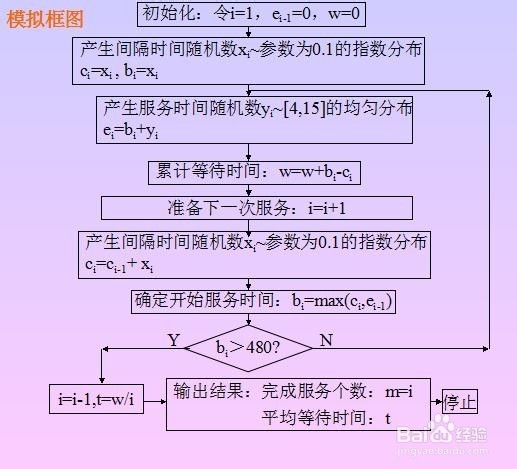10/11

按模型框图编写MATLAB程序，结果如下图所示。

11/11

运行结果如图所示。

注意事项

编写较为复杂的程序，最好事先画出算法框图。

matlab