先把二重积分化简成分步积分，再把y当做常数做一步；出来再把x当做常数再做一步就完了。

为x^2/2+xy，取x=1，x=0想减，得(x+y)dx=1/2+y-0=1/2+y，然后再对y积分，即(1/2+y)dy在(0,1)上的积分。为y^2/2+1/2*y，取y=1,y=0想减，即得到原式=1。

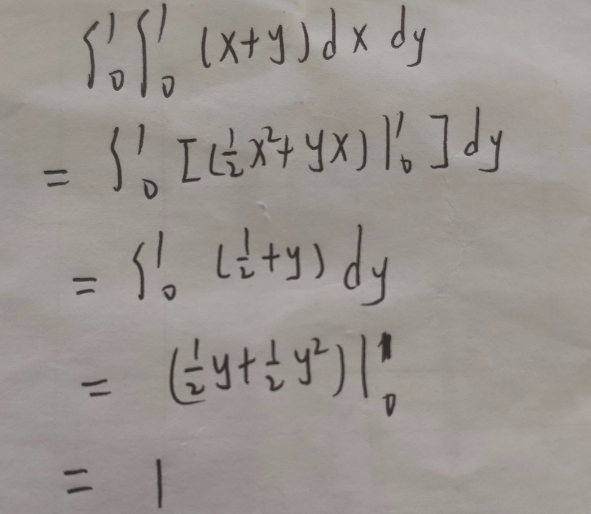
意义

当被积函数大于零时，二重积分是柱体的体积。

当被积函数小于零时，二重积分是柱体体积负值。

在空间直角坐标系中，二重积分是各部分区域上柱体体积的代数和，在xoy平面上方的取正，在xoy平面下方的取负。某些特殊的被积函数f（x，y）的所表示的曲面和D底面所为围的曲顶柱体的体积公式已知，可以用二重积分的几何意义的来计算。