设A 为n 阶方阵,A不等于0 ,若A2次方-3A=0 .证明A-3E 不可逆.
来源:网络收集 点击: 时间:2024-08-11【导读】:
A^2-A-2E=0推出A^2-A=2E,所以A(A-E)=2E,从而A的逆矩阵为1/2(A-E)。
A^2-A-2E=0推出A^2-A-6E=-4E,所以(A+2E)(A-3E)=-4E,从而A+2E的逆矩阵为-1/4(A-3E)。
其中A和B为矩阵。其广义特征值(第二种意义)λ 可以通过求解方程(A-λB)ν=0,得到det(A-λB)=0(其中det即行列式)构成形如A-λB的矩阵的集合。其中特征值中存在的复数项,称为一个“丛(pencil)”。
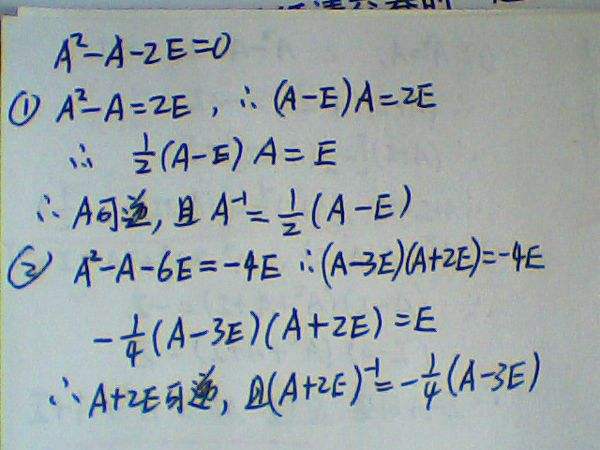
性质定理
1、可逆矩阵一定是方阵。
2、如果矩阵A是可逆的,其逆矩阵是唯一的。
3、A的逆矩阵的逆矩阵还是A。记作(A-1)-1=A。
4、可逆矩阵A的转置矩阵AT也可逆,并且(AT)-1=(A-1)T (转置的逆等于逆的转置)
版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_1107170.html
上一篇:爱安吉消费券怎么使用
下一篇:18年最新兰州办理摩托车驾照及上牌流程
 订阅
订阅