订阅【Mathematica】LogisticSigmoid函数简介
来源：网络收集 点击： 时间：2024-08-31【导读】：
LogisticSigmoid函数，简写为σ函数。那么，这个函数有些非常有趣的性质。我们来一一介绍。工具/原料more电脑Mathematica方法/步骤1/7分步阅读
2/7
3/7
4/7
5/7
6/7
7/7
这个函数表现为S形曲线：
Plot
2/7它是单调递增函数：
In:= D // FunctionExpand // Simplify
Out= E^x/(1 + E^x)^2
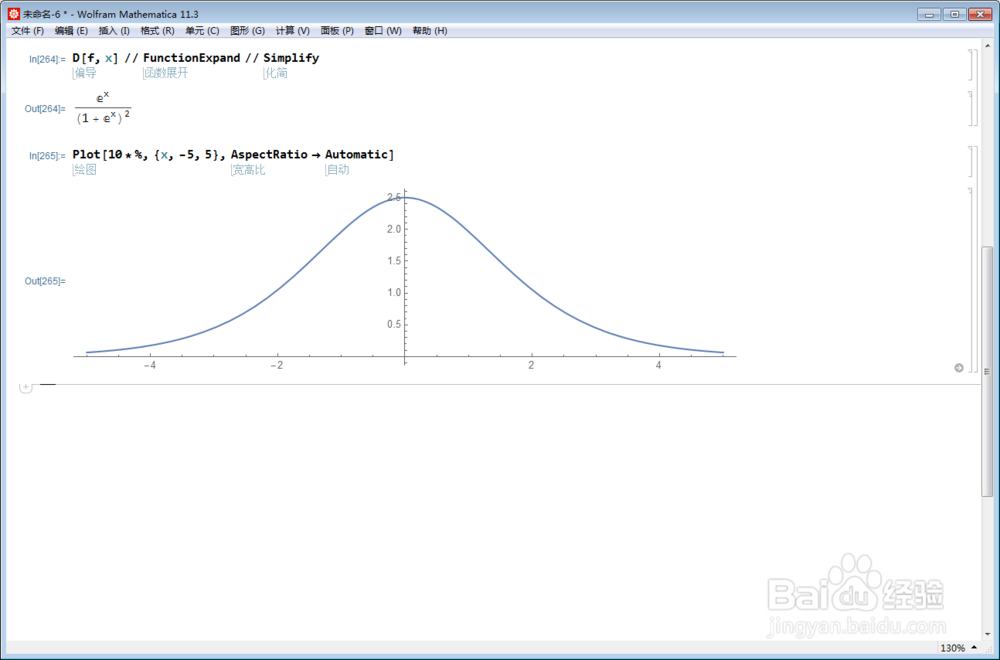3/7它的值域是，以y=0和y=1为渐近线：
In:= Limit
Out= 0
In:= Limit
Out= 1
4/7它是中心对称图形，左侧是下凹曲线，右侧是上凸曲线：
In:= D // FunctionExpand // Simplify
Out= -((E^x (-1 + E^x))/(1 + E^x)^3)
5/7它可以把所有数据归拢到0和1之间，且不同的数据，仍旧不同：
In:= data = RandomReal
Out= {0.143454, 4.77656, 1.28397, 0.799853, 4.48448, 9.89067,
9.6725, 7.84665, 2.66615, 7.23431}
In:= LogisticSigmoid /@ data
Out= {0.535802, 0.991645, 0.783125, 0.689943, 0.988843,
0.999949, 0.999937, 0.999609, 0.935, 0.999279}
6/7与此功能类似的函数，可以是ArcTan：
7/7对比一下这两个函数的图像：
Plot/Pi + 1, 2 f}, {x, -2, 2}, AspectRatio - Automatic]
版权声明：
1、本文系转载，版权归原作者所有，旨在传递信息，不代表看本站的观点和立场。
2、本站仅提供信息发布平台，不承担相关法律责任。
3、若侵犯您的版权或隐私，请联系本站管理员删除。
4、文章链接：http://www.1haoku.cn/art_1179081.html
上一篇：剑三三国古战场怎么打
下一篇：Excel怎么设置图表背景颜色
