是傅立叶变换满足的一个重要性质。

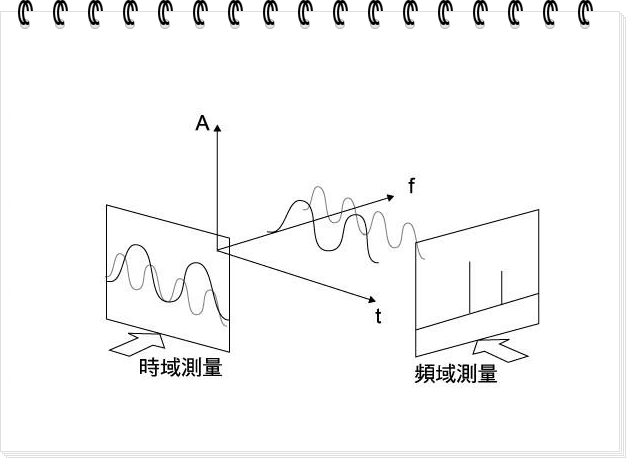
频域卷积定理表明，时域中两个信号的积对应于两个信号的傅立叶变换的卷积除以2Л。

卷积定理揭示了时间域与频率域的对应关系。这个定理适用于Laplace变换、Z变换、Mellin变换和其它傅立叶变换的变化。应该注意的是，以上写法仅适用于特定形式的转换，因为转换可能以其它方式进行规范化，从而使得上面的关系式中出现其它的常数因子。

扩展信息：

卷积定理的应用在许多有关积分变换和积分方程的文章中都有反映。常见的一些重要的积分变换，例如：Mellin变换、Laplace变换、Fourier变换等都具有所谓的卷积性质（Convolution Property）。

这里要注意的是，针对不同的积分变换，卷积性质的形式不是完全相同的，只要一些基本的结构得到保留就可以了。卷积定理还可以简化卷积的运算量。对于长度为 n的序列，按照卷积的定义进行计算，需要做2n-1组对位乘法，其计算复杂度为O（n·n）。

参考资料来源：百度百科-卷积定理

参考资料来源：百度百科-卷积