因为对一元函数来讲，可导必可微，可微必可导。但对多元函数来讲，可微是可偏导的充分不必要条件。

可微是总体的、一般的、关于多的性质，可导是单一的、特殊的、关于“多”中的一的性质。一般成立，特殊必然成立；特殊成立，一般不一定成立，但特殊是一般的基础。在一元函数框架下，多即是一，那么特殊和一般在此条件下得到了统一。

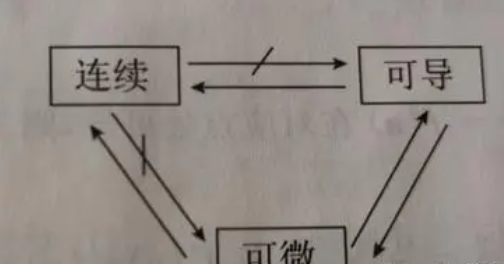
可微条件

1、必要条件

若函数在某点可微分，则函数在该点必连续；若二元函数在某点可微分，则该函数在该点对x和y的偏导数必存在。

2、充分条件

若函数对x和y的偏导数在这点的某一邻域内都存在，且均在这点连续，则该函数在这点可微。