f(z)=1/5*。因为1|z|2，所以|z/2|1，|1/z|1。前两项，提出一个1/z，化成-z/z*1/(1+1/z)和2/z*1/(1+1/z)。

1/(1+1/z)就用公式1/(1-z)=1+z+z+...展开，用-1/z去换z即可。

第三项，提一个1/2，变成-1/2*1/(1-z/2)，同样套上面的公式，只不过这次是用z/2去换z。三项都展开为幂级数之后，一般情况下你是没有办法合并成为一个幂级数的，所以一般来说写到这一步就完成了。当然你也可以把这个幂级数的前面几项写出来，后面打上省略号。

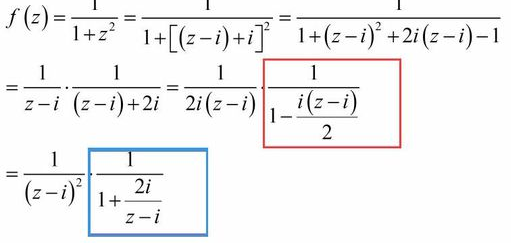
扩展资料：

积分路径γ是位于圆环A内的一条逆时针方向的可求长曲线，把c包围起来，在这个圆环内是全纯的（解析的）。的洛朗级数展开式在这个圆环内的任何地方都是正确的。

在右边的图中，该环用红色显示，其内有一合适的积分路径 。如果我们让是一个圆 ，其中 ，这就相当于要计算的限制到上的复傅里叶系数。这些积分不随轮廓的变形而改变是斯托克斯定理的直接结果。

在实践中，上述的积分公式可能不是计算给定的函数系数最实用的方法；相反，人们常常通过拼凑已知的泰勒展开式来求出洛朗级数。因为函数的洛朗展开式只要存在就是唯一的 ，实际上在圆环中任何与相等的，以上述形式表示的给定函数的表达式一定就是的洛朗展开式。

参考资料来源：百度百科-洛朗级数