有时候，求一个图形的周长是一件略为棘手的事情。如果你有此方面的困扰，赶紧阅读本经验吧。本经验将向你介绍几种图形周长的计算方法，包括：矩形、正方形、圆、直角三角形、普通三角形以及正多边形。方法 1: 矩形1/2分步阅读

求出矩形两条邻边的长，即宽和高的长度。同一平面内，两组对边长度分别相等、四个角均为直角的平行四边形是矩形。由于矩形的对边平行且相等，所以矩形邻边的长度不同，其中一条边称为宽，另一边是矩形的高。（如果矩形的邻边长度相等，图形为正方形。求正方形周长请跳至“正方形”部分）。

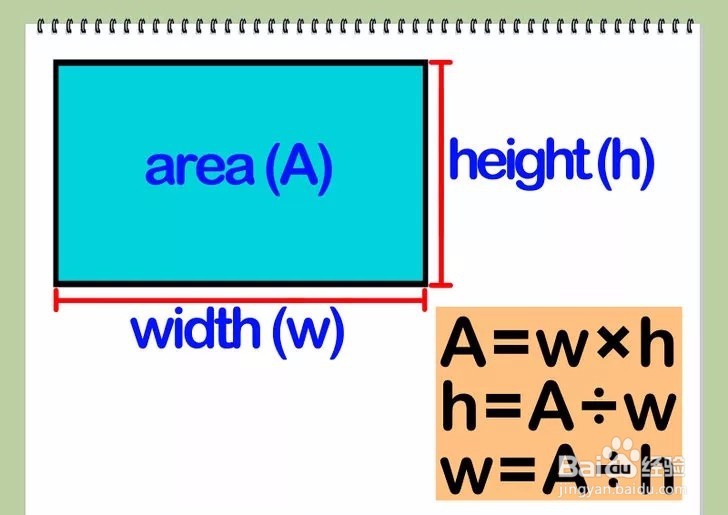
如果你已知矩形的面积和其中一条边长，你可以通过面积公式A=wh求另一边的长度。通过对公式进行简单的代数变换，就得到h=A/w和w=A/h。所以，如果你知道矩形的高和面积，用面积除以高就能得到宽的长度。你也可以用面积除以宽求得高的长度。

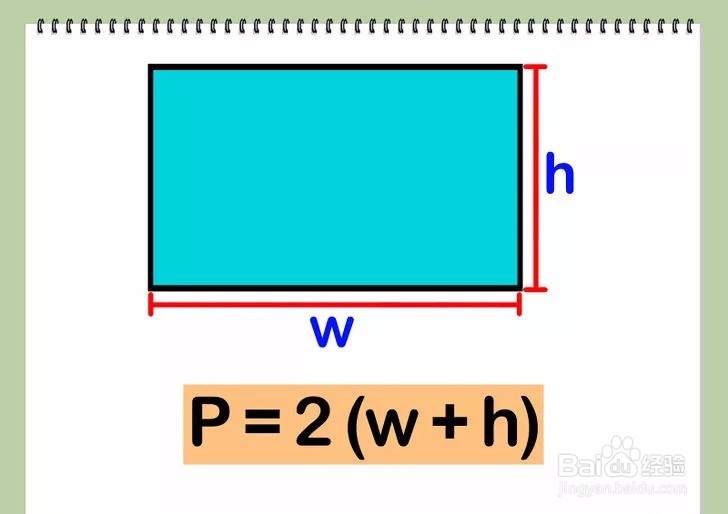
2/2

将宽和高的长度相加，再将得到的结果乘以2就能得到矩形的周长。如果w=宽、h=高，那么矩形的周长(P)的计算公式是P=2(w+h)。

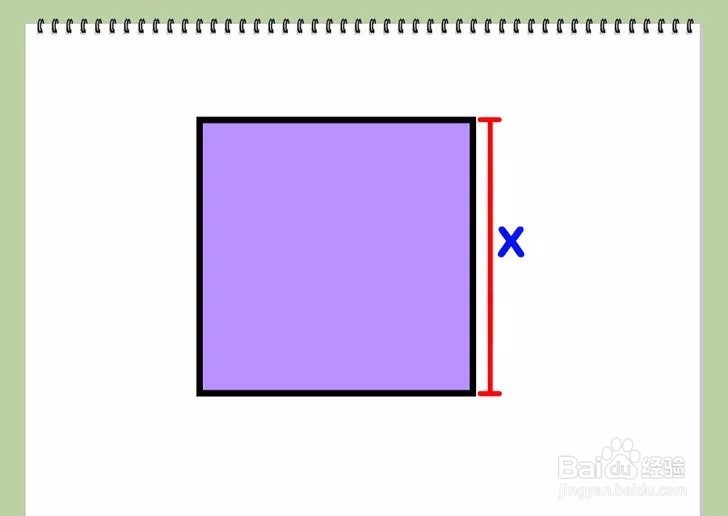
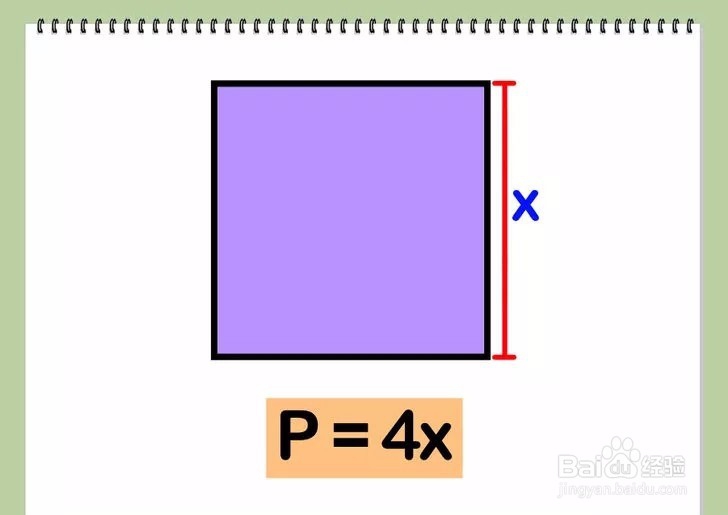
方法 2: 正方形1/3

求出正方形一条边的长度—我们可以称此边长为x。根据定义，我们知道正方形的四条边长度相等。

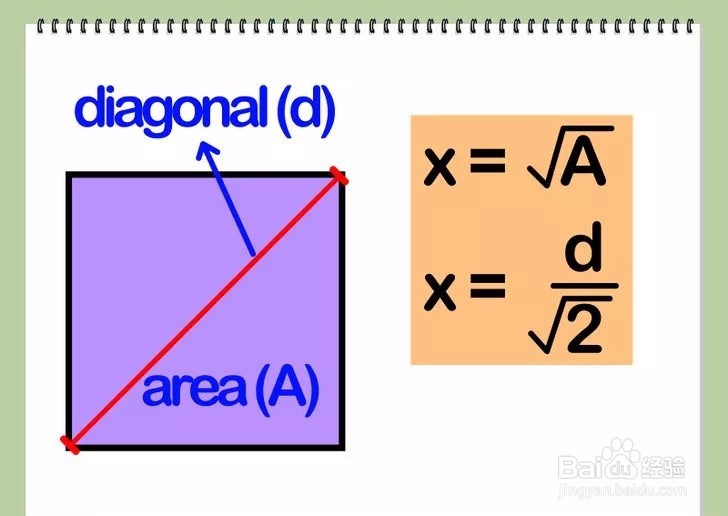
2/3

如果你只知道正方形的面积(A)，那么你可以通过对面积求平方根求得正方形的边长。公式是x=√(A)。

如果你只知道正方形对角线(d)的长度，那么你用d除以2的平方根(√(2)或20.5—两种表示方法皆可)就能得到正方形的边长。公式为x=d/(√(2))。

3/3

将边长乘以4就可求得周长。由于正方形的四条边长度相等，所以周长就是边长的4倍。公式为P=4x。

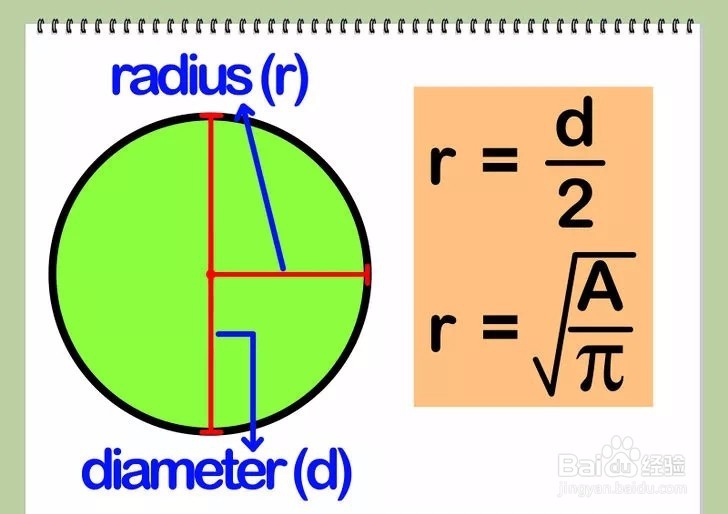
方法 3: 圆形1/2

求圆的半径长r。半径长是从圆心出发到圆的任一点位置的距离。

1、如果你已知圆直径(d)的长度，那么你将直径长d除以2就可得到半径长度。公式为r=d/2。

2、如果你已知圆的面积(A)，那么先将圆的面积除以π，然后再取上步除法结果的平方根，即可得到半径的长。公式为r=√(A/π)。

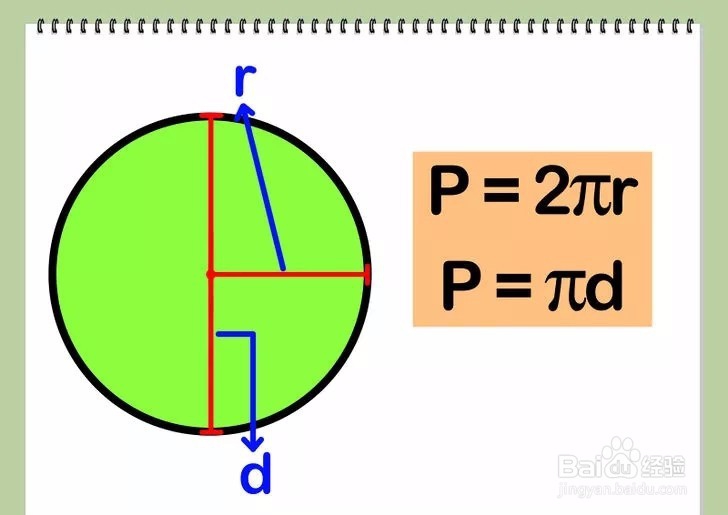
2/2

将半径长r乘以2π即可求得圆的周长。公式为P=2πr。

由于直径的长度是半径的两倍，所以圆周长的公式可以表示为P=πd。

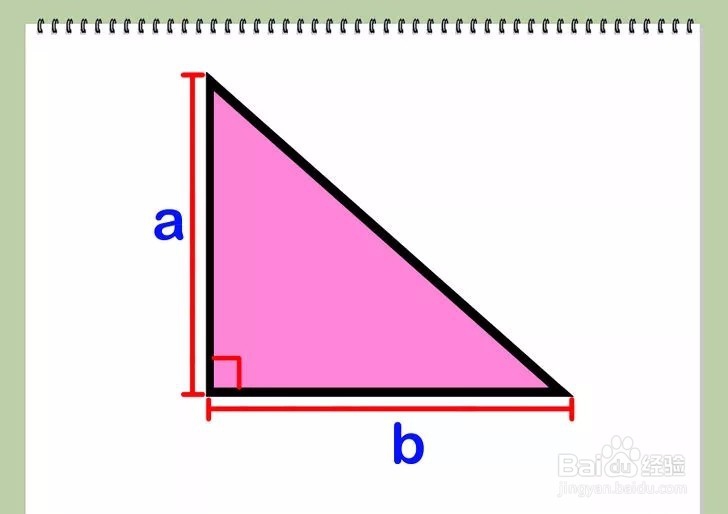
方法 4: 直角三角形1/3

求直角三角形两条短边的长度，表示为a和b。这两条边形成的角是一个直角。

2/3

先求两边长a和b的平方和，然后将结果开平方根求得c。公式为√(a2+b2)。根据勾股定理可知，a2+b2=c2（c是直角三角形的斜边长，也是直角所对的三角形最长边的边长）。

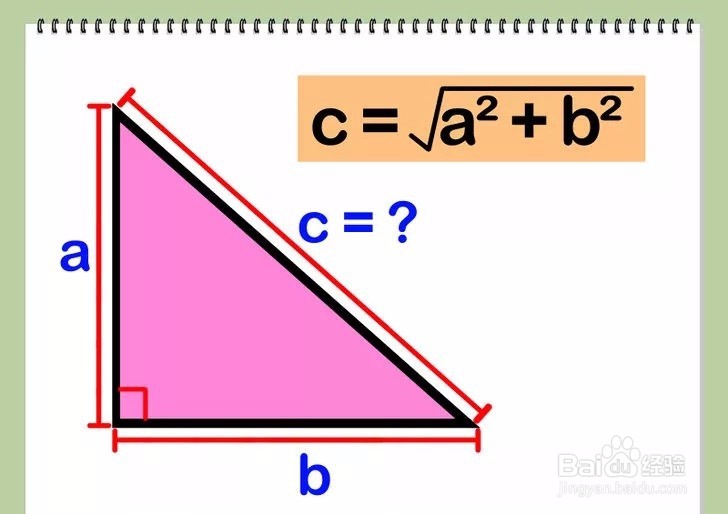3/3

此时你已知三角形三边a, b,和c的值，将三个边长相加即为周长。公式为P=a+b+c。

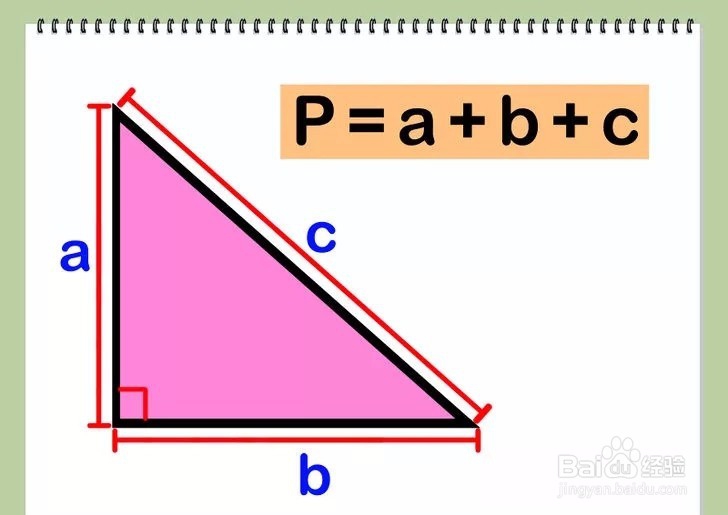方法 5: 普通三角形1/4

求三角形的底边长(x)和对应的高(y)。高是三角形的顶点到底边的距离，高是从三角形的顶点到底边的最短距离，所以高垂直于底边。

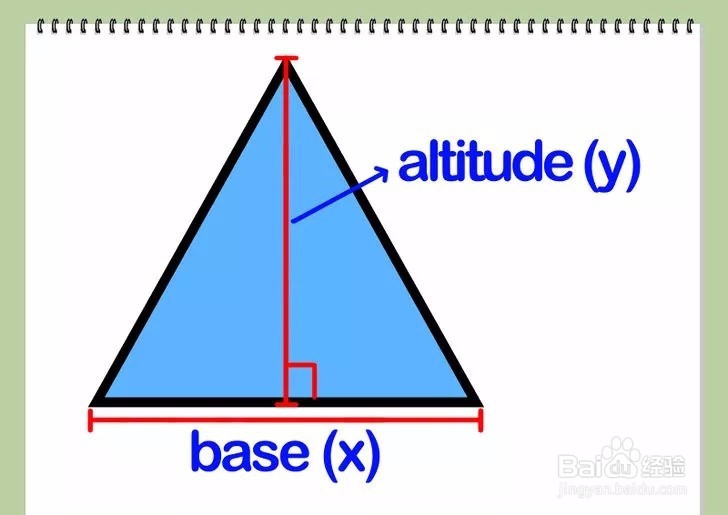2/4

求出底边被高分成的两部分的长度，即x和x，满足x=x+x。高将三角形分成两个直角三角形（一个由x和y标注，一个由x和y标注），而你需要求出这两个直角三角形斜边的长，即c和c(通常用c来标注直角三角形的斜边)。

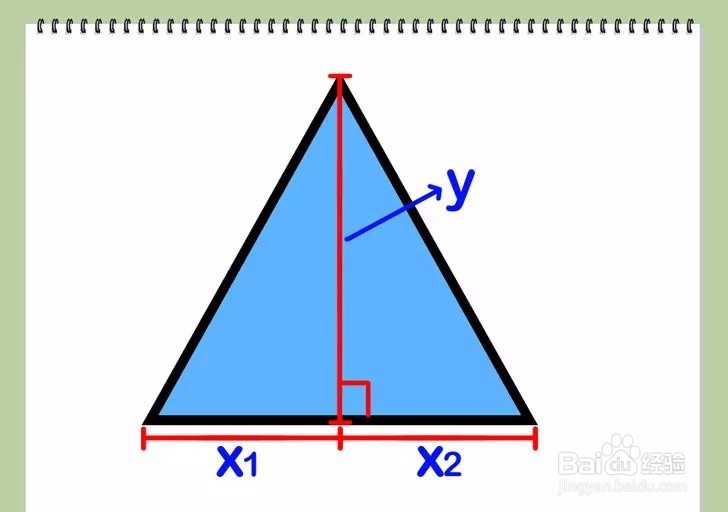3/4

求c和c。利用勾股定理a2+b2=c2，将x代入a,，y代入b，c代入c，然后再将x，y，c分别代入。

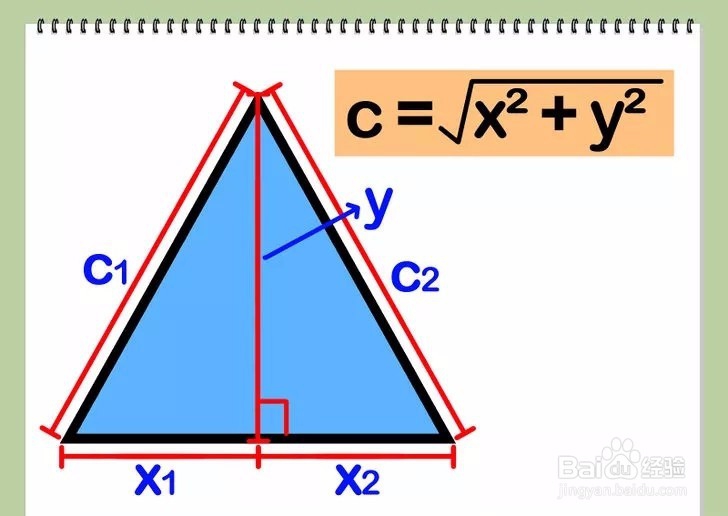4/4

求x，c，c的和，即三角形的周长。

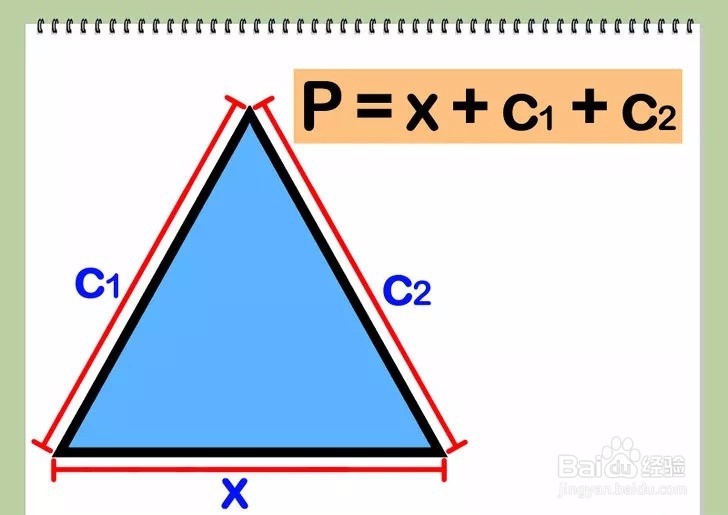方法 6: 正多边形1/2

求正多边形一条边的长。根据定义，正多边形是各条边长度都相等的多边形。

1、如果你知道多边形的边心距（旁切圆的半径：多边形的中心到任意一条边中点的距离），你也可以求出多边形的边长。已知多边形的边心距，则多边形的边长为x=2Atan(180/n)。

2、如果你知道多边形的半径（中心到多边形顶点的距离），你也可以求出边长。已知半径为r，则边长为x=2rsin(180/n)。

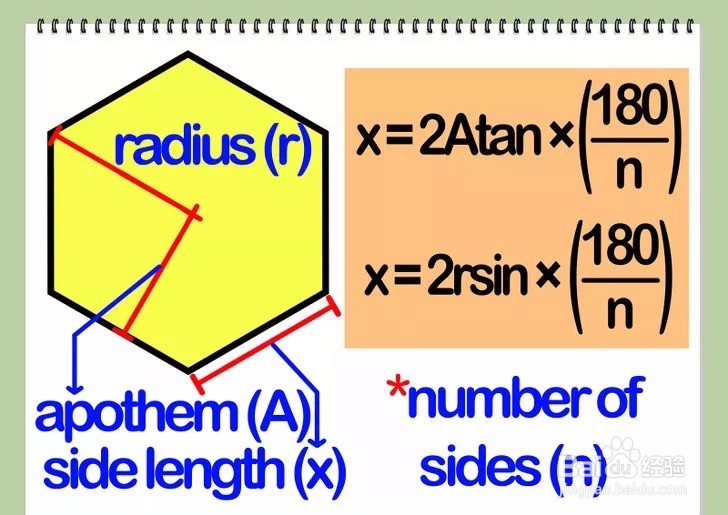2/2

用多边形的边长乘以多边形边的个数。即，一个n变形，边长为x，则周长P=nx。

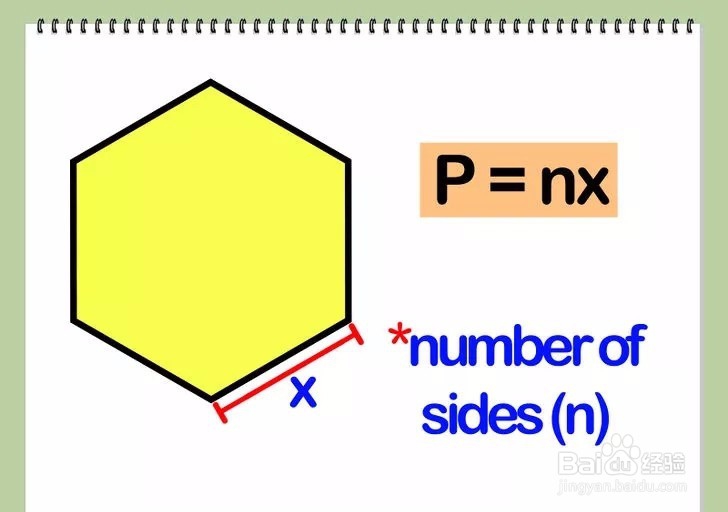注意事项

如果您觉得本经验对您有帮助，请投上您的一票。非常感谢哦！

学习教育交流数学求周长