订阅运筹学大M法例第一第二种解法（两阶段法）
来源：网络收集 点击： 时间：2024-03-11【导读】：
在前面的介绍中，我对题目求解的方法是引入人工变量“M”进行求最优解的，那么这篇将为你介绍一下两阶段法。方法/步骤1/7分步阅读
4/7
5/7
6/7
7/7
注意事项
两阶段法：
第一阶段，不考虑原问题是否存在基可行解，给原线性规划问题加入人工变量，并构造仅含人工变量的目标函数和要求实现最小化。
第二阶段，将第一阶段计算得到的最终表，除去人工变量。将目标函数行的系数，换原问题的目标函数系数，作为第二阶段计算的初始表。
2/7题目如下：
Max Z= 2*x1+ 3*x2- 5*x3;
s.t.
3/7第一步就是转换原来目标函数的形式，将原题目转变为下式之后，进行计算。
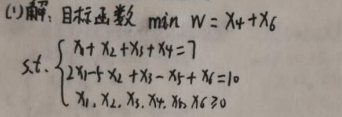4/7由上图得到下面这个单纯形表，然后开始迭代计算，在这里我们需要注意的是，由于目标函数为“Min W”所以我们这次要选择的cj-zj最小值为出基变量即“-3”再由b/（-3）所在列的最小值，确定出基变量，这里确定的出基变量为“2”
5/7进行细心，仔细的迭代过程之后，我们得到下列图示，然后进行下一步迭代。
6/7迭代知道cj-zj都大于零为止，在这，我们可以看到迭代的最终结果中，x4和x6所对应的值都为0，所以原线性规划问题存在基可行解然后进入下一步。
7/7除去人工变量，将目标函数行的系数，换原问题的目标函数系数，然后进行计算。在这，由于改变成原线性规划问题系数之后，cj-zj系数都小于零，就不用在继续进行迭代计算了。结果如下图所示：
注意事项由于目标函数为“Min W”所以我们这次要选择的cj-zj最小值为出基变量，不在是原来的依据最大值确定出基变量了。
一定要注意第一阶段和第二阶段的转换。
版权声明：
1、本文系转载，版权归原作者所有，旨在传递信息，不代表看本站的观点和立场。
2、本站仅提供信息发布平台，不承担相关法律责任。
3、若侵犯您的版权或隐私，请联系本站管理员删除。
4、文章链接：http://www.1haoku.cn/art_318900.html
上一篇：如何让毛孔自由呼吸
下一篇：烧脑大师海底的秘密怎么过关？
