如何在matlab中使用向量乘积和转置?
来源:网络收集 点击: 时间:2024-02-13长度相同的行向量和列向量可以按任一顺序相乘。其结果是一个标量(称为内积)或一个矩阵(称为外积):
u = ;
v = ;
x = v*u

 2/10
2/10对于实矩阵,转置运算对 a ij 和 a ji 进行交换。对于复矩阵,还要考虑是否用数组中复数项的复共轭来形成复共轭转置。MATLAB 使用撇号运算符 () 执行复共轭转置,使用点撇号运算符 (.) 执行无共轭的转置。对于包含所有实数元素的矩阵,这两个运算符返回相同结果。
3/10示例矩阵 A = pascal(3) 是对称的,因此 A 等于 A。然而,B = magic(3) 不是对称的,因此 B 的元素是 B 的元素沿主对角线反转之后的结果:
B = magic(3)
 4/10
4/10X = B
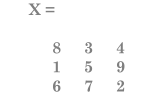 5/10
5/10对于向量,转置会将行向量变为列向量(反之亦然):
x = v
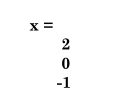 6/10
6/10如果 x 和 y 均为实数列向量,则乘积 x*y 不确定,但以下两个乘积
x*y
和
y*x
产生相同的标量结果。此参数使用很频繁,它有三个不同的名称内积、标量积或点积。甚至还有一个专门
的点积函数,称为 dot。
7/10对于复数向量或矩阵 z,参量 z 不仅可转置该向量或矩阵,而且可将每个复数元素转换为其复共轭数。也就是说,每个复数元素的虚部的正负号将会发生更改。以如下复矩阵为例:
z =
 8/10
8/10z 的复共轭转置为:
z
 9/10
9/10非共轭复数转置(其中每个元素的复数部分保留其符号)表示为 z.:
z.
 10/10
10/10对于复数向量,两个标量积 x*y 和 y*x 互为复共轭数,而复数向量与其自身的标量积 x*x 为实数。
MATLAB版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_33512.html
 订阅
订阅