MATLAB教学视频：常微分方程（组）在MATLAB中的求解方法，视频时长约115分钟，通过具体的案例，首先讲解了MATLAB dsolve函数求特定形式的微分方程（组）解析解，并分析了dsolve函数的局限性；然后着重讲解了使用MATLAB ODE系列函数，求解一阶和高阶微分方程（组）数值解的通用方法。工具/原料moreMATLABode函数，dsolve函数MATLAB教学视频：常微分方程（组）在MATLAB中的求解方法1/9分步阅读

教学内容

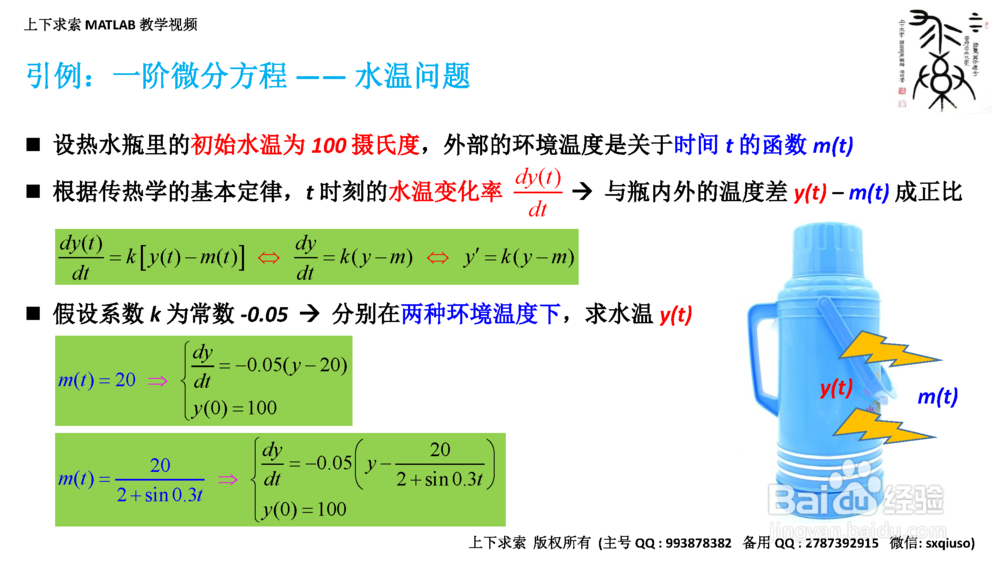
1. 引例：一阶微分方程——水温问题

2. 引例：二阶微分方程——范德波尔方程

3. MATLAB dsolve求微分方程的解析解

4. MATLAB dsolve求微分方程组的解析解

5. 微分方程(组) 的MATLAB 数值解法

5.1 一阶微分方程的数值解法

5.2 一阶微分方程组的数值解法

5.3 二阶/ 高阶微分方程的数值解法

5.4 二阶/ 高阶微分方程组的数值解法

6. 课程总结

2/9

引例：一阶微分方程—— 水温问题

3/9

MATLAB dsolve 求微分方程的解析解

MATLAB dsolve 函数的基本调用格式

1.S = dsolve (eqn, cond)

2.S = dsolve (eqn, cond, v)

4/9

引例：二阶微分方程—— 范德波尔方程

5/9

MATLAB dsolve 求微分方程组的解析解

MATLAB dsolve 总结

1. 倘若求解成功，得到的是精确的解析解

2. 高等数学：仅有特定形式的微分方程(组) ，才有解析解

3. 没有解析解的微分方程(组)：dsolve 无能为力

4. 抛弃dsolve：更加实用的数值解

6/9

微分方程 (组) 的MATLAB 数值解法

MATLAB 求解微分方程 (组) 的数值解：ODE (Ordinary Differential Equation) 系列函数

1. 非刚性问题：ode45 / ode23 / ode113

2. 刚性问题：ode15s / ode23s / ode23t / ode23tb

3. 优先尝试使用ode45：基于显格式的 (4, 5) 阶龙格— 库塔算法

4.如果ode45 计算失败，再尝试其他的 ode 函数

5.基本调用格式： = odexx (odefun, tspan, y0)

7/9

一阶微分方程的数值解法

一阶微分方程组的数值解法

8/9

二阶/ 高阶微分方程的数值解法

9/9

课程总结

1. 存在解析解的特定形式的微分方程(组)

1.1 dsolve求解析解

1.2 ODE函数求数值解

2. 不存在解析解的微分方程(组)

2.1 只能使用ODE函数求数值解

2.2 高阶的微分方程(组)：降阶处理：一阶微分方程组

3. 本课程未做讨论的几个重要的数学问题数值算法课程

3.1 微分方程(组) 的数值解：近似解：MATLAB ODE 函数求解精度如何？

3.2 数值算法的收敛性和稳定性

3.3 刚性问题 非刚性问题

注意事项

常微分方程组的求解，请尽量使用数值解法

高阶微分方程组，需要做降阶处理，才能使用MATLAB的ODE函数求解