当矩阵（方阵）A为行列式不为0的矩阵时，也就是说方阵A是可逆矩阵的，那么A为非奇异矩阵。对于非奇异矩阵A可以进行LU分解，即把A分解为一个变换形式的下三角矩阵L（进行了行变换）和一个上三角矩阵U，使得A=L*U。同时得到线性方程组的解为X=U\(L\b)，其中b为线性方程组等号右边的常数构成的列向量。本文将演示MATLAB利用LU分解法求解线性方程组的方法。工具/原料moreMATLAB = lu(A)方法/步骤1/6分步阅读

第一，下图是要求解的线性方程组，参考了王正林等《MATLAB科学计算》有关内容。

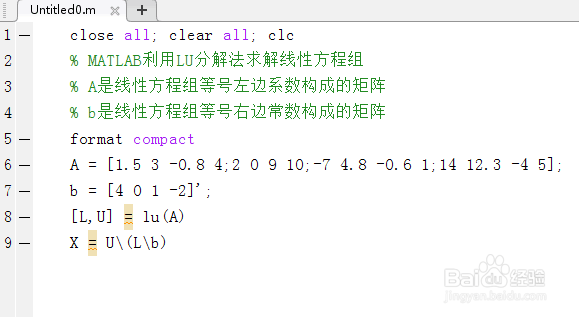
2/6

第二，启动MATLAB，新建脚本，输入如下代码：

close all; clear all; clc

% MATLAB利用LU分解法求解线性方程组

% A是线性方程组等号左边系数构成的矩阵

% b是线性方程组等号右边常数构成的矩阵

format compact

A = ;

b = ;

= lu(A)

X = U\(L\b)

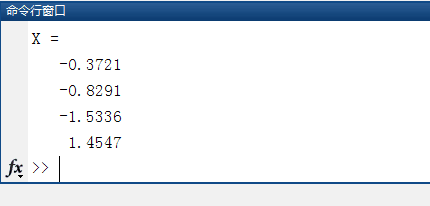
3/6

第三，保存和运行上述代码。得到线性方程组的解如下：

X =

-0.3721

-0.8291

-1.5336

1.4547

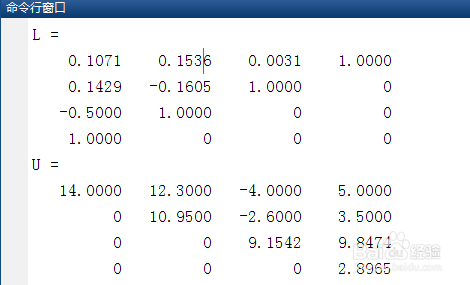
4/6

第四，其中lu分解法得到了一个变换形式的下三角矩阵L（进行了行变换）和一个上三角矩阵U如下：

L =

0.1071 0.1536 0.0031 1.0000

0.1429 -0.1605 1.0000 0

-0.5000 1.0000 0 0

1.0000 0 0 0

U =

14.0000 12.3000 -4.0000 5.0000

0 10.9500 -2.6000 3.5000

0 0 9.1542 9.8474

0 0 0 2.8965

5/6

第五，对变换形式的下三角矩阵L（进行了行变换）和上三角矩阵U进行验证，即L*U是否等于A，在命令窗口输入L*U，回车得到如下结果，可以见A=LU。这里需要注意的是L*U，而不是L.*U，.*表示的矩阵每一项元素相乘，*表示矩阵相乘。

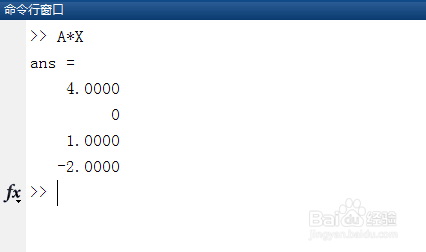
6/6

第六，对解进行验证，在命令行窗口输入A*X，回车得到如下结果，可见A*X=b，即结果正确，说明LU分解法求解线性方程组的方法是有效的。

MATLAB线性方程组分解法求解