【微分几何】椭球面怎么进行Gauss变换?
来源:网络收集 点击: 时间:2024-04-04【导读】:
Gauss变换,指的是针对某个三维正则曲面(处处存在法向量),把曲面上每一个点的单位法向量的起点平移到原点,终点形成的曲面。正则曲面经过Gauss变换,得到的新的曲面一定是球面上的一部分。本文就用Mathematica来画出椭球面经过Gauss变换之后的曲面。工具/原料more电脑Mathematica方法/步骤1/5分步阅读 2/5
2/5 3/5
3/5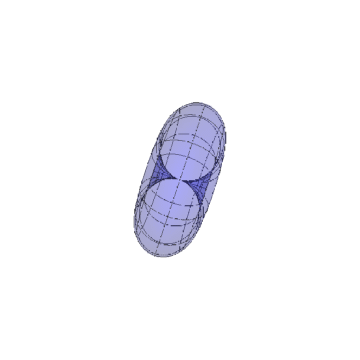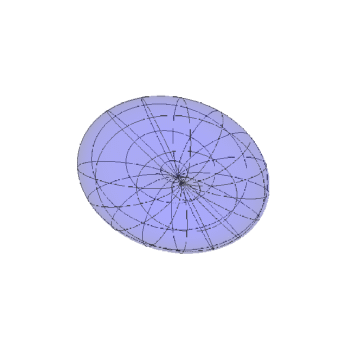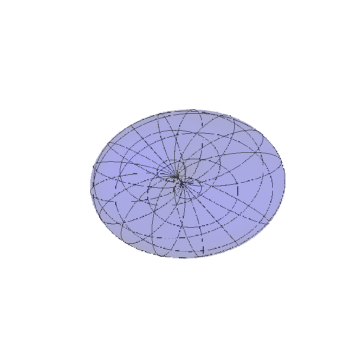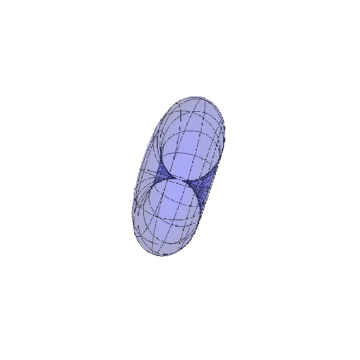 4/5
4/5

 5/5
5/5

椭球面的参数方程可以是?:
r := {Cos Cos, Cos Sin, Sin}*{3, 4, 5}
.
这个椭球面没有焦点了。
 2/5
2/5Gauss变换的过程:
ru = D, u];
rv = D, v];
计算法向量:
uv = Cross;
把法向量化为单位向量:
uv/Sqrt
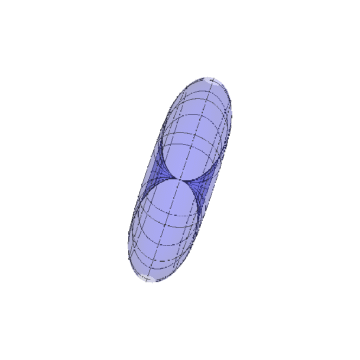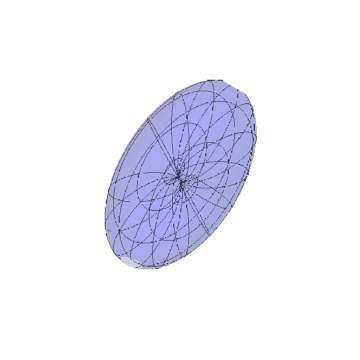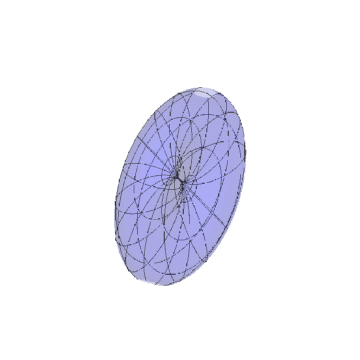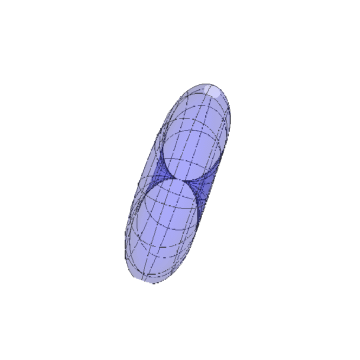
把归一化的法向量视为新区面的参数方程,得到一个类似于球面的曲面。
.
这个球面中间有一个空腔?
 3/5
3/5如果直接把向量uv视为新区面的参数方程,得到的曲面如下。
可以看到,中间真的存在凹陷。
 4/5
4/5椭球面:
{Cos Cos, Cos Sin, Sin}*{3, 3, 5}


 5/5
5/5椭球面:
{Cos Cos, Cos Sin, Sin}*{5, 3, 5}



版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_419499.html
上一篇:怎样画小巫女?
下一篇:vegas 19视频编码器voukoder设置中文界面方法
 订阅
订阅