【平面几何】50°与30°的角格点三角形
来源:网络收集 点击: 时间:2024-04-08【导读】:
一道平面几何题目如下图所示:△ABC,∠A=100°,∠ACB=30°,延长AC至D,使CD=AB,求∠ADB的度数。本文,介绍一个简洁的纯几何证明方法。工具/原料more电脑网络画板方法/步骤1/6分步阅读 2/6
2/6 3/6
3/6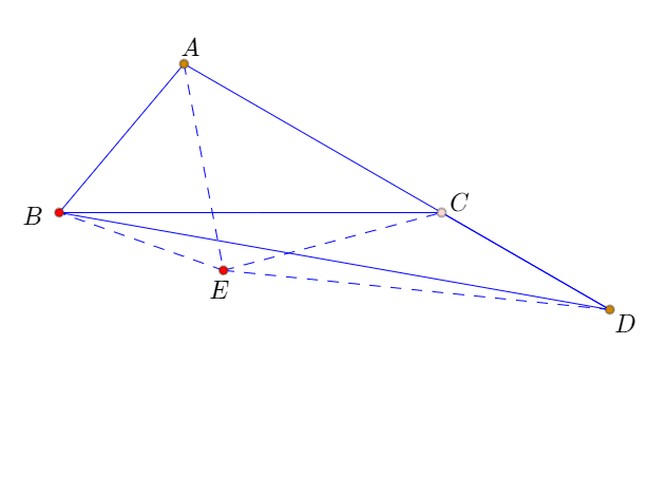 4/6
4/6 5/6
5/6 6/6
6/6
作正三角形ABE,使得C、D、E三点位于直线AB同侧。
注意,E实际上位于线段BD上,但这一点需要证明,所以作图的时候,特意把E点画在BD之外。
 2/6
2/6连接CE。
注意到∠ACB=∠AEB/2,且EA=EB,所以C点位于圆上。
这个圆以E为圆心、AB为半径。
这个圆图中未画出。
 3/6
3/6连接DE,此时可以确定:
AB=BE=AE=CE=CD。
 4/6
4/6因为∠EAB=60°,所以∠EAC=40°,又因为AE=CE,所以∠AEC=100°。
 5/6
5/6因为CE=CD,而补角∠ACE=40°,所以∠AED=∠ADE=20°。
 6/6
6/6此时,已经可以证明B、E、D共线了。
整个题目证明如下:

版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_473267.html
上一篇:学历在线验证报告怎么获取
下一篇:被贬低怎么办
 订阅
订阅