【平面几何】两角共用一条角平分线模型
来源:网络收集 点击: 时间:2024-04-12【导读】:
本文,介绍一个有趣的平面几何模型,共平分线角模型。工具/原料more电脑网络画板方法/步骤1/7分步阅读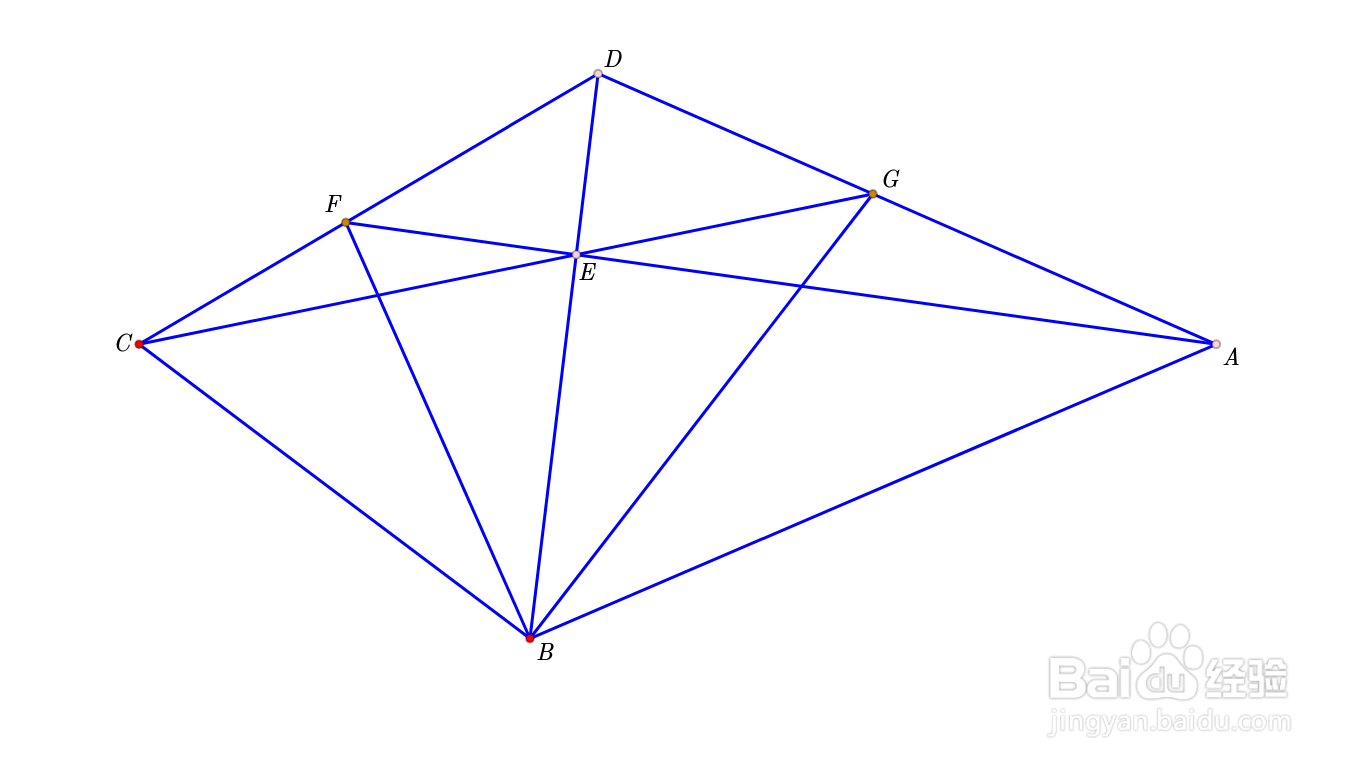 2/7
2/7 3/7
3/7 4/7
4/7 5/7
5/7 6/7
6/7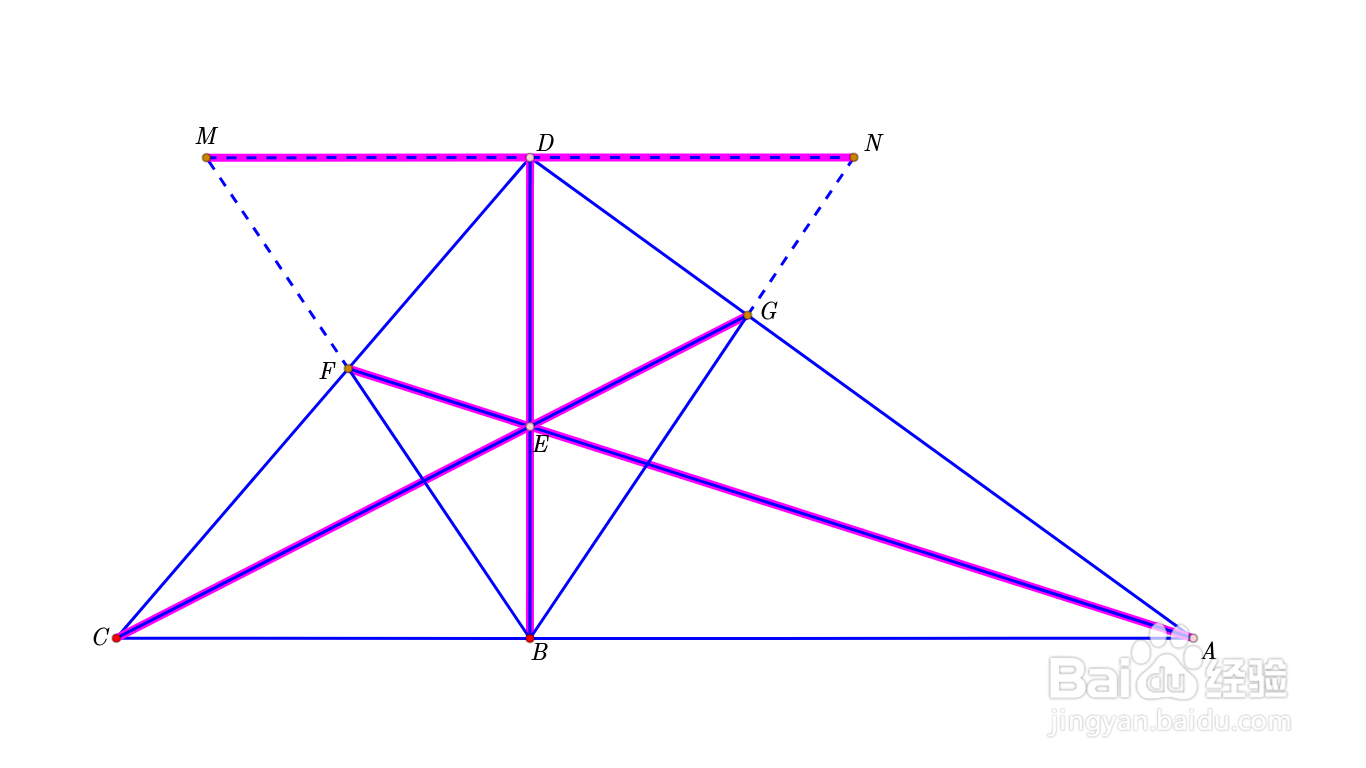 7/7
7/7 注意事项
注意事项
模型如下图所示:
E是∠ABC的角平分线BD上一点,且不与B和D重合,直线AE和CD交于F,直线CE和AD交于G,那么BD也是∠FBG的角平分线。
 2/7
2/7这个模型,当∠ABC是平角的时候,就变成了与三角形有关的一个几何问题:
DB⊥AC于B,E是直线BD上且不与B和D重合,直线AE和CD交于F,直线CE和AD交于G,那么BD也是∠FBG的角平分线。
 3/7
3/7我们来证明步骤2的模型。
过D作直线AB的平行线,分别与BF、BG交于M、N。
 4/7
4/7因为MD//BC,所以MD/BC=DF/CF。
依据是平行线截线段成比例。
 5/7
5/7同样的,有DN/AB=DG/AG。
 6/7
6/7根据【塞瓦定理】,可知(DF*CB*AG)=(DG*AB*CF);
把步骤4和5的结论,代入到上式,可以发现,MD=DN。
 7/7
7/7注意到BD⊥AC,AC//MN,所以BD⊥MN;
又因为MD=BD,所以,BD是线段MN的垂直平分线;
所以,BD平分∠MBN,也就是平分∠FBG。
至此,步骤2里面的模型,就证明出来了。
 注意事项
注意事项步骤1里面的模型,是步骤2的模型的一般情形,你会证明吗?
版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_498972.html
上一篇:马蜂蛹怎么吃
下一篇:PPT演示文档如何插入椭圆形对话气泡
 订阅
订阅