【抽象代数】主理想整环
来源:网络收集 点击: 时间:2024-04-15一个整环是主理想整环,如果它的所有理想都是主理想。
 2/7
2/7Z不是主理想整环。
反设由x和2生成的理想(x,2)是主理想,
那么存在元素d(x),使得(x,2)=(d(x)),那么:
(x,2)=Z。
但是注意,1不在(x,2)里面,导致矛盾。
 3/7
3/7主理想整环R的每个既约元是素元。
假设p是既约元,但是不是素元,那么(p)就是极大理想,所以R/(p)是一个域。
p不是素元,那么必定存在m和n,使得p|mn,但是p∤m且p∤n;
进而,(m+(p))(n+(p))=mn+(p)=(p)。
由于域里面没有零因子,所以有(m+(p))=(p)或(n+(p))=(p),与p∤m且p∤n矛盾。
 4/7
4/7假设一个整环R有无限个理想 I1、I2、I3……,满足:
I1⊂I2⊂I3⊂……,
我们说,这个整环存在一个理想的无限升链。
令I=I1∪I2∪I3∪……,那么,I也必定是R的一个理想。
注意,I1∪I2=I2、I1∪I2∪I3=I3……
 5/7
5/7主理想整环R不存在理想的无限升链。
反设I1⊂I2⊂I3⊂……是R的无限升链,那么I=I1∪I2∪I3∪……就是R的一个理想,进而I是主理想,记I=(a)。
设a∈In,有(a)⊂In;
另外,In⊂I=(a),所以,(a)=In,与无限升链的假设矛盾。
 6/7
6/7综合步骤3和步骤5,可以证明,主理想整环是唯一因子分解整环。
7/7Gauss整数环是主理想整环。
假设N是Z的一个理想,a是N中绝对值最小的非零元;
任取N的元素b,有b/a=u+vi∈Q;
分别选择最接近u、v的整数m、n,有|b/a-m-ni|1;
显然,b-a*(m+ni)∈N;
但是,|b-a*(m+ni)|=|a|*|b/a-m-ni||a|,所以b-a*(m+ni)=0;
b=a*(m+ni)∈(a),所以,N=(a)。
这样,我们间接证明了,Gauss整数环是唯一因子分解整环。
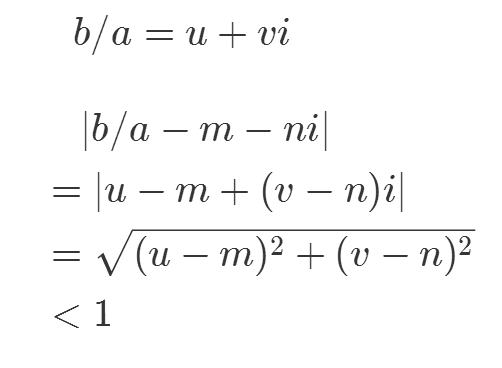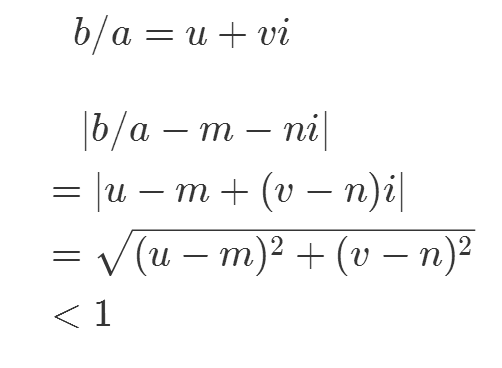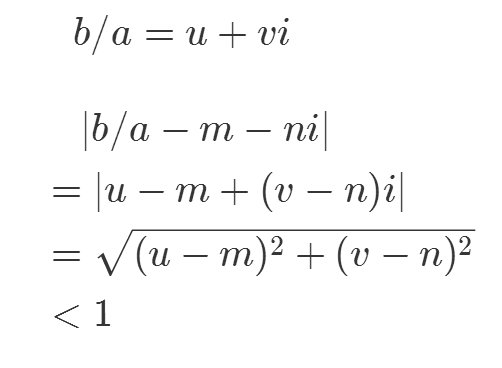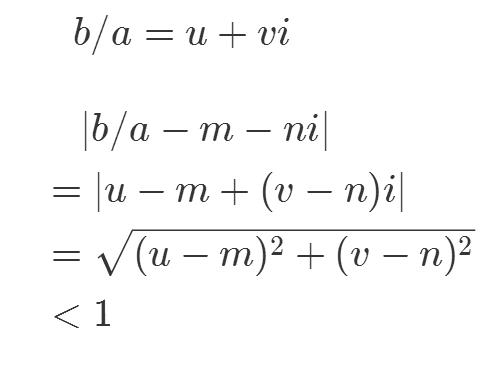
版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_514215.html
 订阅
订阅