订阅【微分几何】双曲抛物面的Gauss变换
来源：网络收集 点击： 时间：2024-04-16【导读】：
本文，演示双曲抛物面的Gauss变换的效果。工具/原料more电脑Mathematica方法/步骤1/6分步阅读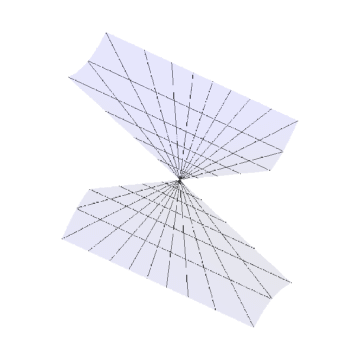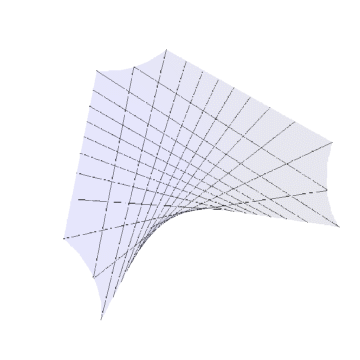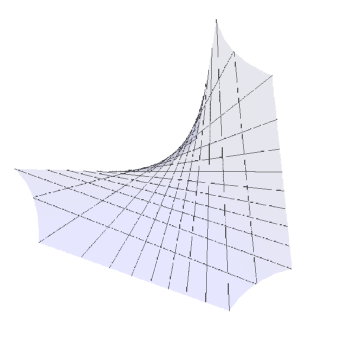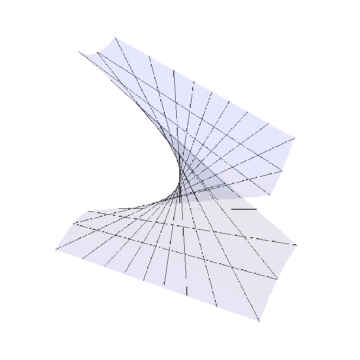
2/6
3/6
4/6
5/6
6/6
注意事项
双曲抛物面的参数方程可以是：
r := {Tan, Tan, Tan Tan}
其中u和v的取值范围是-π/2到π/2。
这是一个无限曲面，我们不可能全部画出来。
2/6Gauss变换之后的曲面图像如下。
偌大的一个双曲抛物面，只留下一个半球形状的曲面。
3/6如果法向量不归一化：
ru = D, u];
rv = D, v];
uv = Cross;
图像仍旧是无限大。归一化的目的，就是把远处的景色拉到近处。
4/6双曲抛物面：
r := {Tan, Tan, 5 Tan Tan - 100}
Gauss变换之后仍旧是半球面。
5/6r := {5 Tan, Tan, Tan Tan}
6/6r := {100 Tan, Tan, Tan Tan}
注意事项各种双曲抛物面经过Gauss变换，只能得到半球面。步骤6里面的结果，可能是绘制的样本数不够，导致图像有缺陷。
版权声明：
1、本文系转载，版权归原作者所有，旨在传递信息，不代表看本站的观点和立场。
2、本站仅提供信息发布平台，不承担相关法律责任。
3、若侵犯您的版权或隐私，请联系本站管理员删除。
4、文章链接：http://www.1haoku.cn/art_527939.html
上一篇：QQ帐号被封停，QQ钱包里的资金怎么办？
下一篇：b站视频怎么设置仅自己可见
