在日常办公和教学中，经常会遇到求最大值的问题，只要精确建立数学模型，然后使用专业的数学软件就能很容易得出结果。如果你的电脑上没有很专业的数学软件，使用excel的线性规划求解工具也能得到你想要的结果。这里，我们以一个企业商品售卖情况为例，计算商品售价的最大值，假设这个企业下面有A、B、C三个公司，A公司每天做出的商品每件可以卖50元，B公司每天做出的商品每件可以卖40元，C公司每天做出的商品每件可以卖60元，A、B、C三个公司每天生产的商品总件数是450，其中A公司的商品不少于100件，B公司的商品不少于60件，C公司的商品不多于50件，求每天企业商品售价获得的的最大值。这里，笔者按照方法步骤做简要介绍。工具/原料moreexcel2007方法/步骤1/11分步阅读

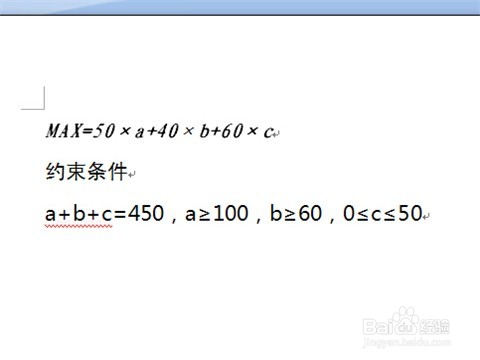
根据题目建立数学模型,假设三个公司售出商品分别是a、b、c件，题目中要求商品售价的最大值，也就是“最大值=50×a+40×b+60×c”，约束条件：a+b+c=450,a≥100，b≥60，0≤c≤50。

2/11

在运用规划求解前，要确定excel是否加载了规划求解工具，许多人在第一次使用这个工具的时候，excel中默认没有加载，这时先单击左上角office按钮，在弹出的菜单中选择“excel选项”。

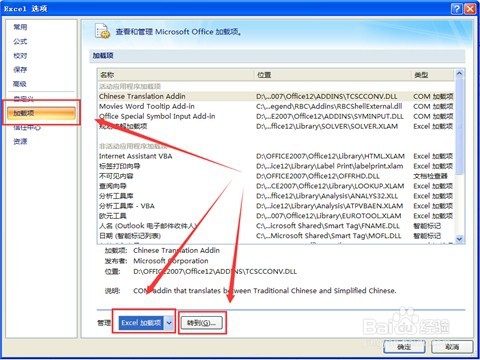
3/11

接着会弹出“excel选项”对话框，选择对话框左侧“加载项”，在右侧弹出的界面下部分管理下拉菜单中选择“Excel加载项”，然后点击“转到...”。

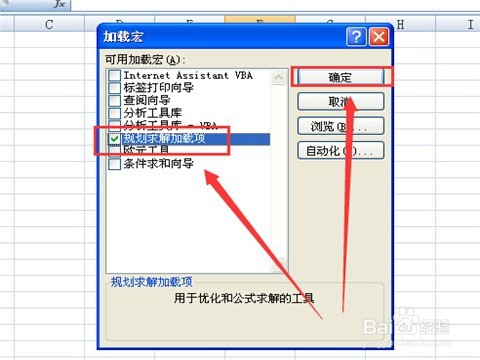
4/11

接着会弹出“加载宏”对话框，勾选下面的“规划求解加载项”，然后点击“确定”，你会发现“规划求解”按钮出现在了“数据”行下面的“分析”面板组上。

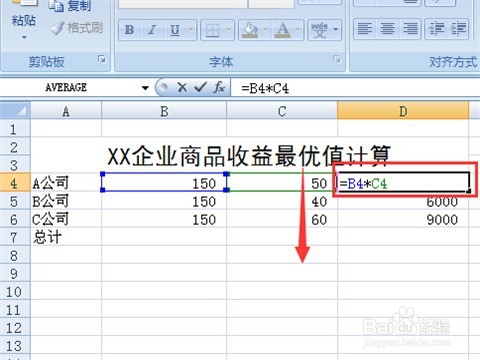
5/11

下面就可以使用规划求解工具了，先按照所建立的数学模型，将相关数值输入excel单元格中，这里要先对a、b、c赋予一个初值，我们选择商品总数450的三分值，即每件商品数量初始值都设为150。如下图所示，单元格D4、D5、D6分别是A、B、C三个公司售出的商品价格总和，即他们对应的前两个单元格的乘积。

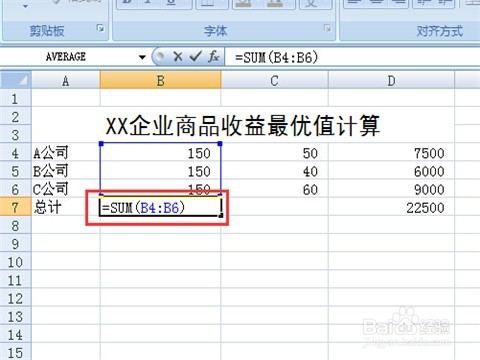
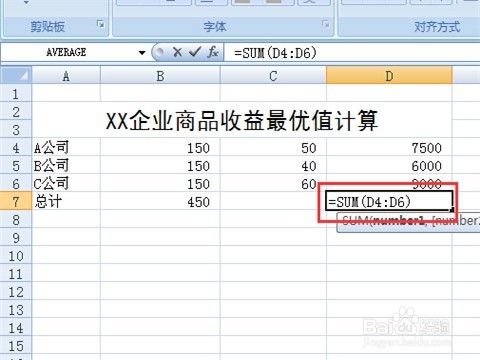
6/11

添加函数或者是公式，这一步非常重要，如果不添加函数或者是公式，即使使用线性规划工具求解，也不会得到收敛的值。先选中B7单元格，根据数学模型可知，这是三种商品数量之和，输入“=SUM(B4:B6)”，同理在D7单元格中输入“=SUM(D4:D6)”。

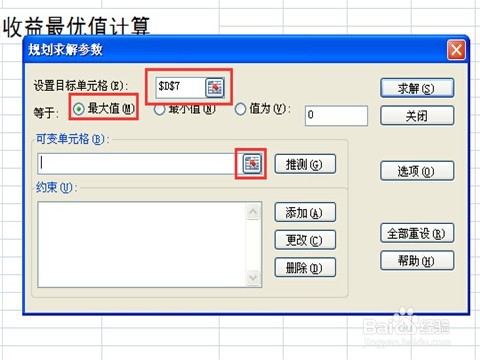
7/11

接着就可以使用线性规划求解工具求解了，先选中商品售出价格总和的单元格，即D7单元格，然后单击“规划求解”按钮，这时会弹出一个“规划求解参数”对话框，我们可以看到“设置目标单元格”已经选中了D7单元格，在下面的求解选项中我们点选“最大值”前面的圆圈。接着需要选择“可变单元格”，点击下边空格最右侧的按钮。

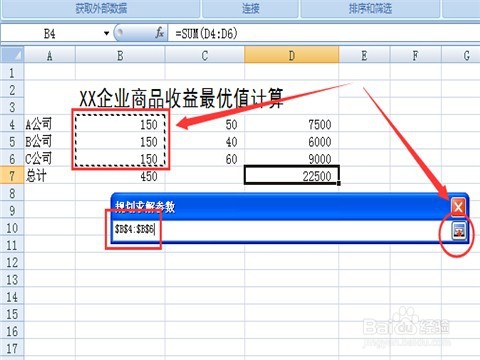
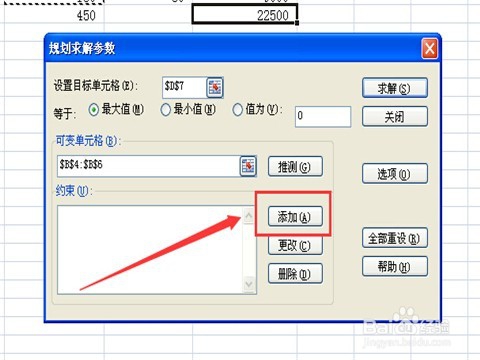
8/11

这时你会发现“规划求解参数”对话框收起来了，这便于你选择单元格。从题目中分析，可变数量就是三种产品卖出的数量，所以选中单元格B4、B5、B6，然后单击空白格右边的按钮，展开“规划求解参数”对话框。然后就是需要添加约束条件了，单击“添加”按钮。

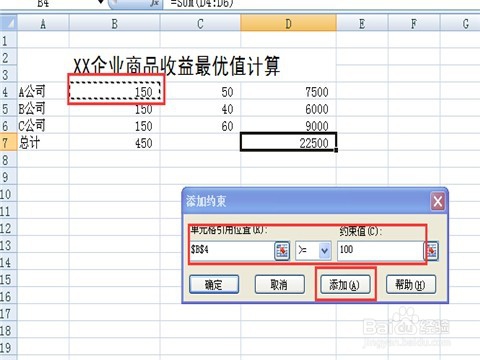
9/11

这时会弹出“添加约束”对话框，按照第一步中所建立的数学模型，逐一添加约束。先选中B4单元格，这时“添加约束”对话框中“单元格引用位置”显示了选中的单元格的位置，然后在后面的下拉菜单中选择“=”，接着在约束值中输入“100”，然后点击“添加”按钮。

10/11

同理，可以添加其它的约束条件，这里特别要注意的是B7单元格的约束值是450，即B7=450，这个约束条件，千万不要忘记输入了。所有约束条件输入完毕后，可以在“规划求解参数”对话框中看到如下结果。然后，再单击“求解”按钮。

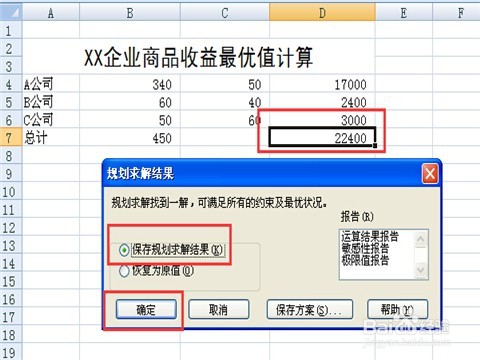
11/11

这时，会弹出一个“规划求解结果”对话框，你可以看到对话框中显示“规划求解找到一解，可满足所有的约束及最优状况”，在下面的选项中点选“保存规划求结果”前面的圆圈，然后单击“确定”按钮，你会发现数据区域的值已经发生了改变，D7单元格的数值就是最终结果。

EXCEL规划工具商品售价最大值