与一元二次方程相关的几何题如何解?
来源:网络收集 点击: 时间:2024-05-03【导读】:
与一元二次方程相关的几何题怎样解?现简述如下。方法/步骤1/7分步阅读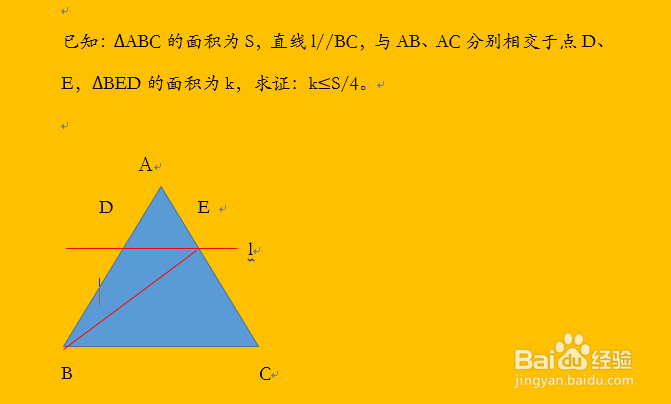 2/7
2/7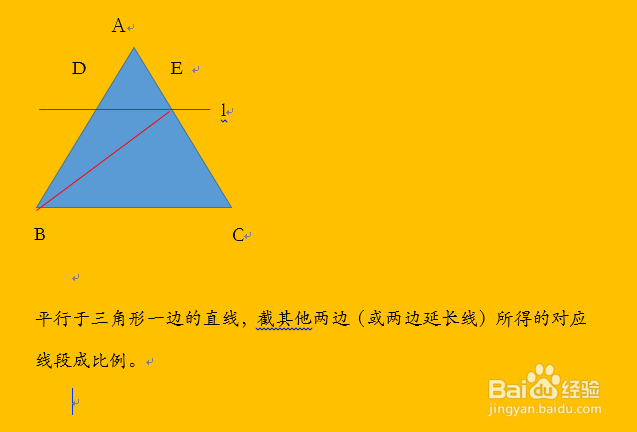 3/7
3/7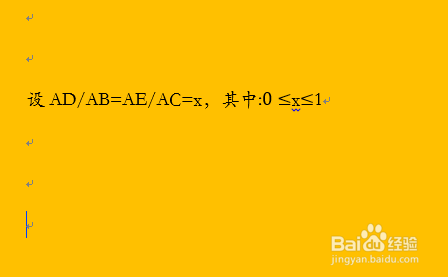 4/7
4/7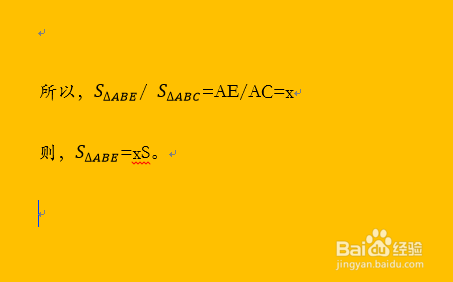 5/7
5/7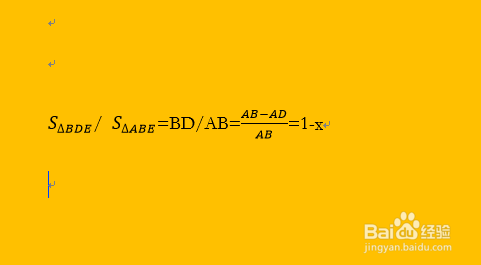 6/7
6/7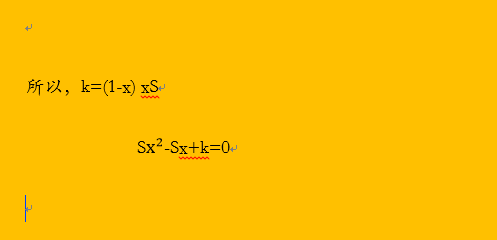 7/7
7/7 注意事项
注意事项
根据几何问题,分析关系后,构造一元二次方程是关键点。
引入例题:
已知三角形ABC的面积为S,直线l平行于BC,与AB、AC分别相交于点D、E,三角形BED的面积为k,求证:k小于等于S/4。
 2/7
2/7根据DE//BC,可以想到【平行线分线段成比例定理】
 3/7
3/7设AD/AB=AE/AC=x,其中x的取值为大于等于0且小于等于1。
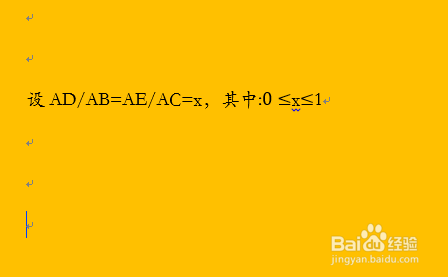 4/7
4/7所以,三角形ABE的面积:三角形ABC的面积=AE:AC=x
则,三角形ABE的面积=xS。
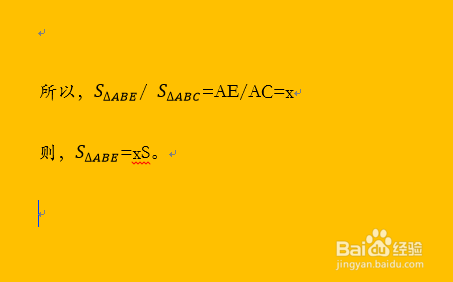 5/7
5/7有,三角形BDE的面积:三角形ABE的面积=BD/AB=(AB-AD)/AB=1-k。
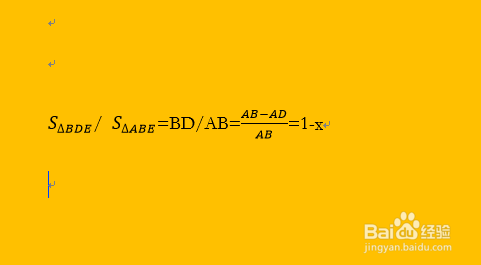 6/7
6/7所以,k=(1-x)*x*S
S*x^2-S*x+k=0
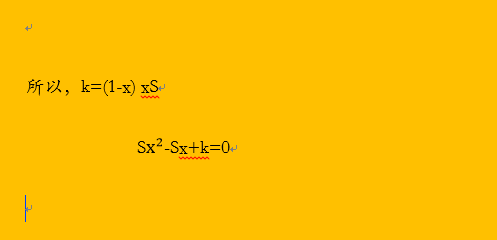 7/7
7/7转化为一元二次方程问题。
由题意得,S^2-4*S*k不小于0。
因为S0,所以,S-4*k不小于0。
则,k小于等于S/4。
 注意事项
注意事项根据几何问题分析关系,构造一元二次方程是关键。
版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_662637.html
上一篇:PS中怎么把文字变粗
下一篇:炸过猪油的猪油渣做什么比较好吃?
 订阅
订阅