用网络画板演示Cayley—Bacharach定理
来源:网络收集 点击: 时间:2024-02-19【导读】:
本文,介绍一下三次曲线理论的一个有趣的定理——Cayley—Bacharach定理:如果两条三次曲线交于9个点,第三条三次曲线过其中八个点,那么它也一定经过第九个点。工具/原料more电脑网络画板方法/步骤1/7分步阅读 2/7
2/7 3/7
3/7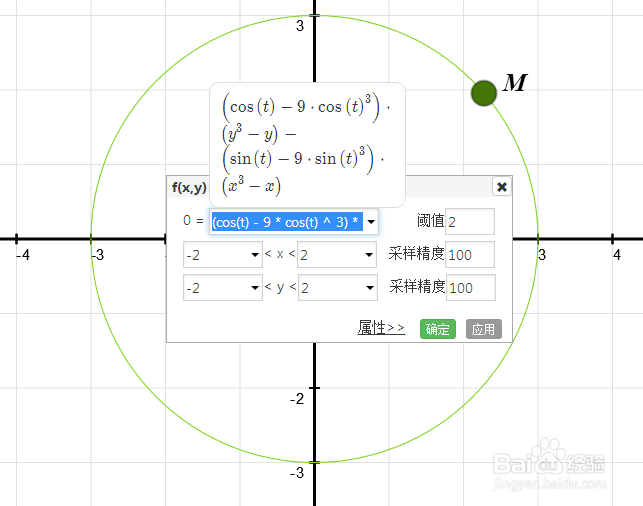 4/7
4/7 5/7
5/7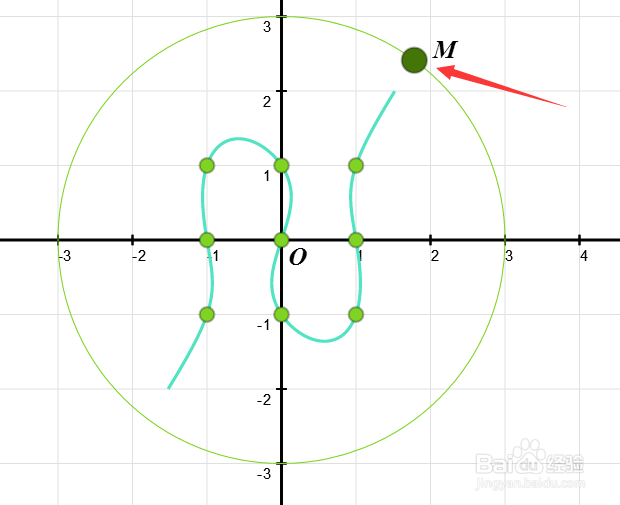 6/7
6/7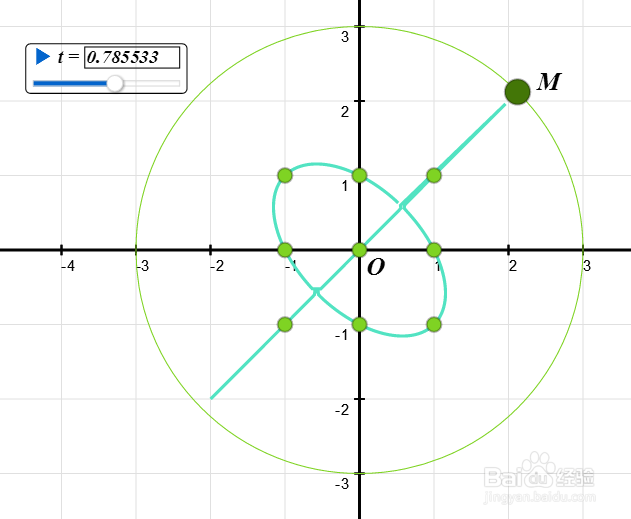 7/7
7/7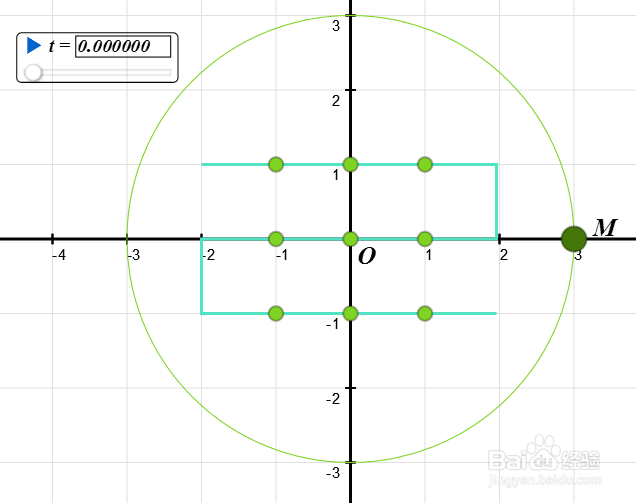
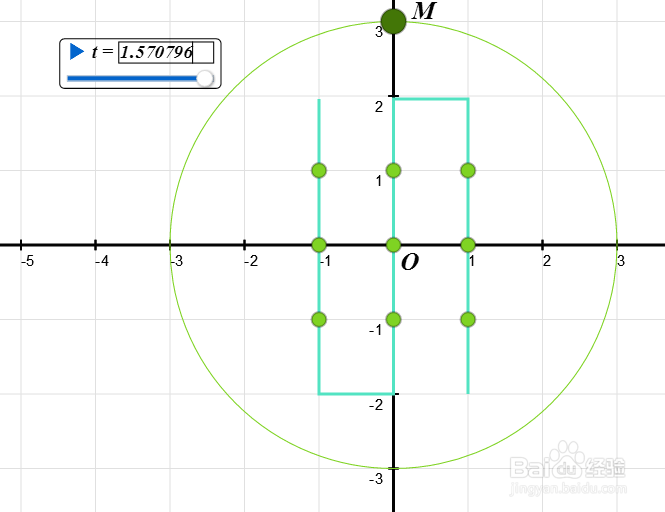
在平面上构造九个点,横坐标和纵坐标分别取值-1、0、1。
 2/7
2/7很明显,这九个点并不能确定一条三次曲线,还需要第10个点。
这第10个点,我们取半径为3的圆上的动点M,圆心位于原点。
过九点的任意三次曲线于这个圆必定有交点,
所以,这个动点M遍历整个圆周之后,三次曲线也遍历了所有情形。
 3/7
3/7根据十个点的坐标,可以求出三次曲线的隐函数方程:
* (y ^ 3 - y)= * (x ^ 3 - x)
作出这个隐函数的图像。
 4/7
4/7把M的属性里面的拖动值和点值都改为t。
 5/7
5/7这样,拖动M,可以改变三次曲线的形状。
 6/7
6/7构造变量t。
当t=pi/4的时候,三次曲线退化为一个椭圆和一条直线。
 7/7
7/7当t等于pi/2的整数倍的时候,三次曲线退化为三条直线。


版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_78865.html
上一篇:百度云APP 磁力链接 在线观看
下一篇:灯笼怎么做简单又漂亮
 订阅
订阅