在Mathematica中，二项分布的符号是BinomialDistribution

二项分布相当于n次独立的概率为p的两点分布结果的和的分布。

其概率函数如图。

Binomial则是计算二项系数（n个里取x个的情况数），即n!/(x!(n-x)!)

如图计算了二项式系数前四项。

二项系数和二项式以及以及杨辉三角联系密切。如图代码显示一个杨辉三角。

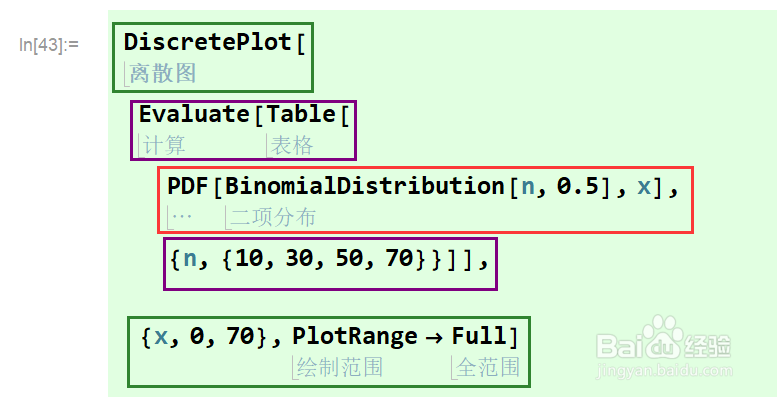
下面，我们使用DiscretePlot函数绘制二项分布B(n,0.5)的分布。

n分别取10，30，50，70.可以看到，n越高，分布越平滑，同时平均值增大。

注意：当我们使用二项分布和二项系数时，不要把Binomial写成Binomal，后者是二元正态分布。是Bi（二元）+normal（正态），而不是Binomial。

二项分布B(n,p)的平均值为np，方差为n(1-p)p。

方差有时也记作npq，p是每一次两点分布为1的概率，q是为0的概率即1-p.

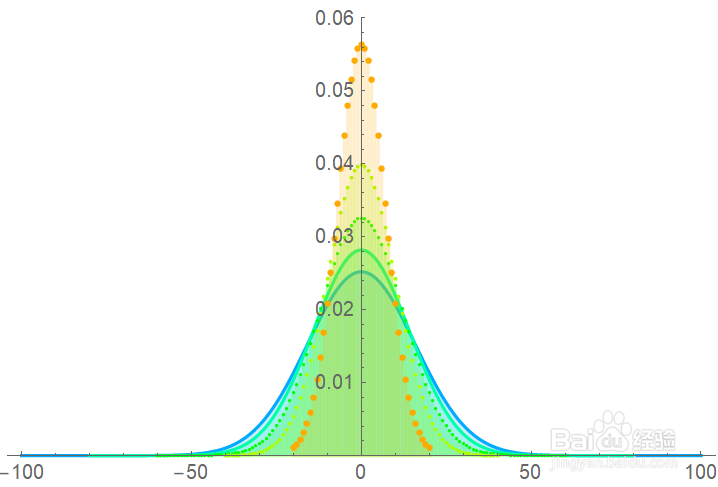
当我们计算(X-n*p)的分布时（X是二项分布B(n,p)），当p不变，n增大时，二项分布逼近正态分布的样子。

（准确的说，变换若取(X-n*p)/Var(X)会趋近于标准正态分布，但是在离散概率下不方便变换和画图）

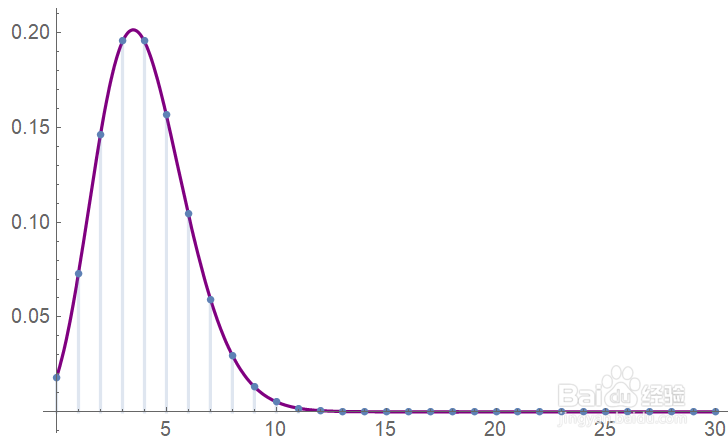
当λ=np为定值时，随着n的增大，p变小，这样的二项分布趋近于泊松分布。

效果如图。实线是泊松分布。

通过概率函数PDF得到的是离散概率分布，只有当离散间隔为1时，才能和连续概率密度函数进行数值上的比较，这很不方便。

因此，我们认为一个离散分布趋近于一个连续分布，可以考察累计分布函数CDF。