【Mathematica】抛硬币实验的概率问题
来源:网络收集 点击: 时间:2024-05-31【导读】:
假设要进行抛硬币试验,实验次数是10000次。那么,其中恰好出现100次证明朝上的概率是多少?工具/原料more电脑Mathematica方法/步骤1/6分步阅读 2/6
2/6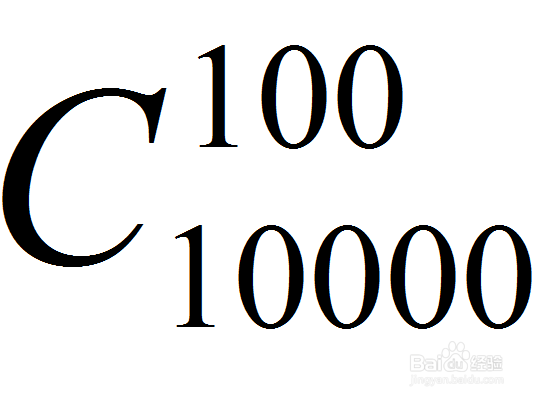 3/6
3/6 4/6
4/6 5/6
5/6 6/6
6/6
每次试验,硬币正面朝上的概率都是0.5,那么,两次实验,硬币的状态可能是:
+-
++
--
-+
其中+表示正面朝上,-表示反面朝上。
那么,其中恰好出现一次正面朝上的概率是0.5=2*(0.5)^2。
 2/6
2/6一万次试验,恰好出现100次正面朝上,有多少种可能呢?
嗯,这可以表示为从10000里面选出100个数,有多少种可能。
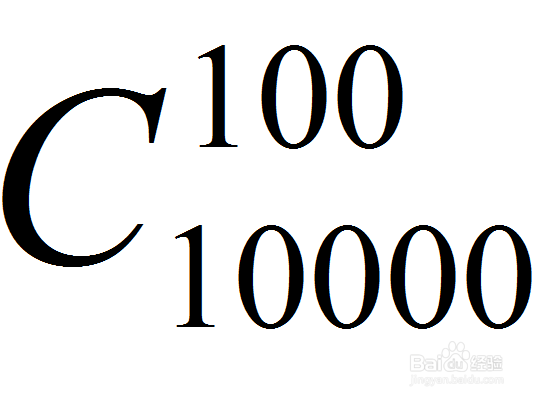 3/6
3/6上面这个数字很大,不过Mathematica可以很快算出来:
Binomial
 4/6
4/6进而可以算出概率:
Binomial*0.5^(10^4)
这个概率很小。
 5/6
5/6换另一种算法:
N*(1/2)^(10^4)]
 6/6
6/6恰好出现5000次的概率是:
N*(1/2)^(10^4)]
约等于0.007979。

版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_864546.html
上一篇:小米平板5pro怎么设置儿童模式
下一篇:梦幻手游三界异闻录卷三攻略大全
 订阅
订阅