这里，我们打算用Mathematica演示一下函数的级数展开式对于该函数的逼近现象。 大家都知道，级数如果是收敛的话，那么项数越多，与对应的函数的误差越小；而Mathematica不仅能够求出函数的各种级数展开，还可以绘制级数的图像，并且能够动态的展示级数与函数的逼近情况！ 开始。工具/原料more电脑Mathematica方法/步骤1/9分步阅读

先来求正弦函数sinx在x=0时的幂级数展开式，且使得级数式取到x^20项（20阶）：

Series, {x, 0, 20}]

2/9

用列表的形式，把sinx的前20阶的幂级数展开式表示出来：

Table, {x, 0, n}], {n, 1, 20}]

3/9

如果感觉有点乱，可以用Column进行排列：

Table, {x, 0, n}], {n, 1, 20}] // Column

这样观察起来就容易多了！

4/9

我们把sinx的前20阶幂级数的余项去掉，便于作图：

Table, {x, 0, n}], {n, 1, 20}] // Column // Normal

Table, {x, 0, n}], {n, 1, 20}] // Normal // Column

大家可以比较一下上面两个代码运行之后的结果，看看有什么区别，并思考一下出现这种区别的原因！

5/9

把sinx的前20阶幂级数的图像画出来，并与sinx的图像加以比较：

Plot, {x, 0, n}]], {n, 1, 20, 1}]], {x, 0,

4 Pi}, PlotRange - 3]

和

Plot, {x, 0, n}]], {n, 1, 20, 1}]], {x, 0,

4 Pi}, PlotRange - 100]

和

Plot,

Evaluate], {n, 1, 20, 1}]]}, {x，0, 4 Pi},

PlotRange - 3]

注意，当PlotRange取到100的时候，sinx的波动几乎就是看不着了！

6/9

用动态图模拟这个逼近过程：

Manipulate, Evaluate, {x, 0, n}]]]}, {x, 0,

10 Pi}, PlotRange - 2]， {n, 1, 20, 1}]

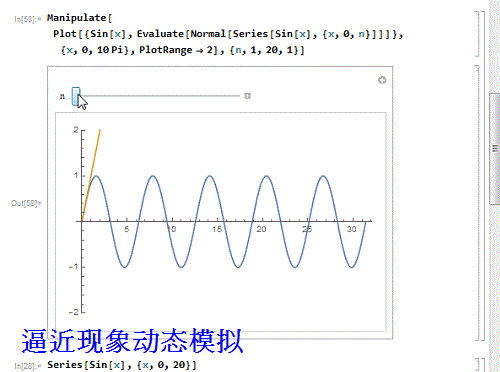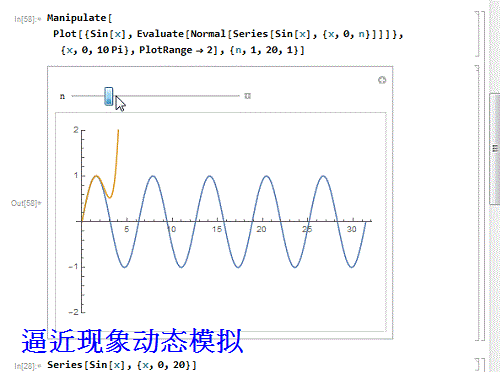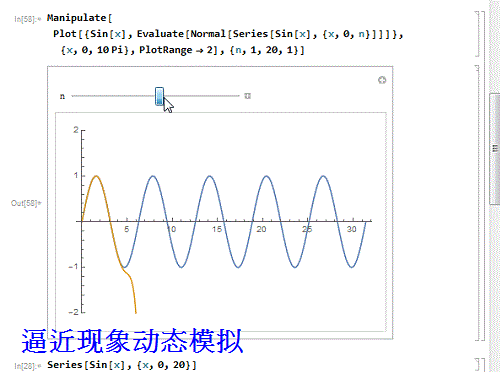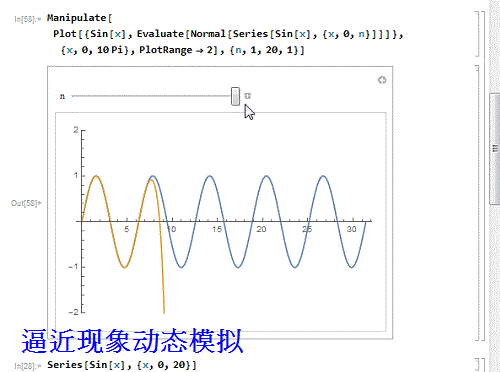7/9

感觉逼近的程度不够？那就要继续增加幂级数的阶数，100阶：

Manipulate, Evaluate, {x, 0, n}]]]}, {x, 0,

10 Pi}, PlotRange - 2], {n, 1, 100, 1}]

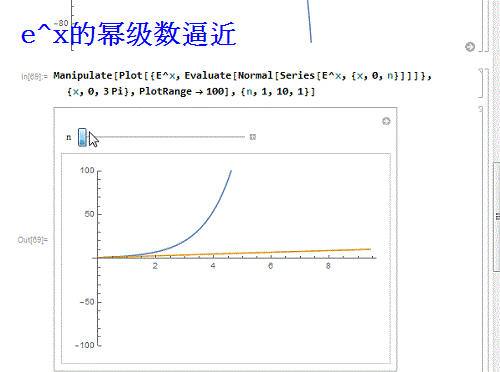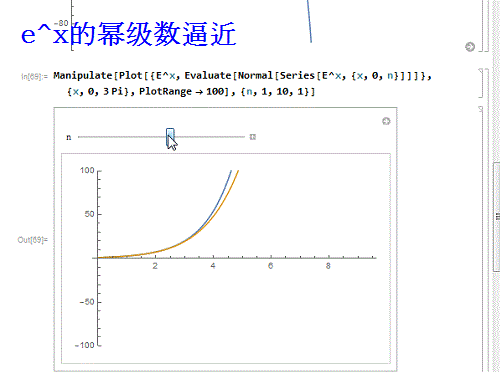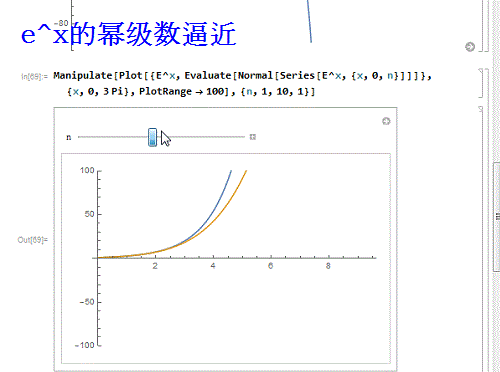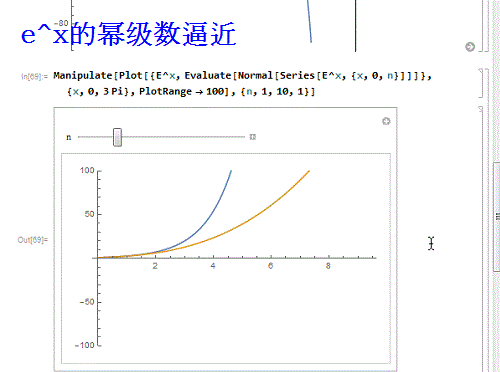
8/9

再换一个函数——e^x：

Manipulate]]}, {x, 0, 3 Pi},

PlotRange - 100], {n, 1, 10, 1}]

e^x和sinx有一个特点，就是它们的幂级数处处收敛！

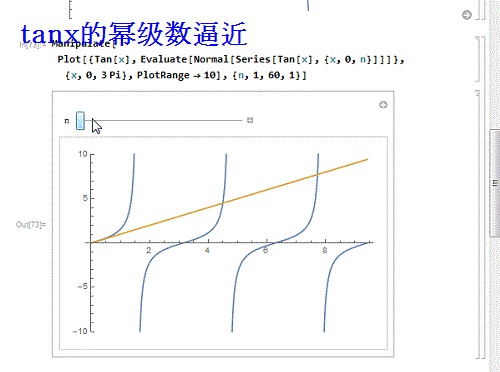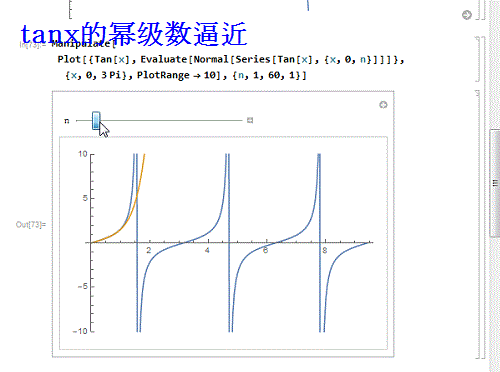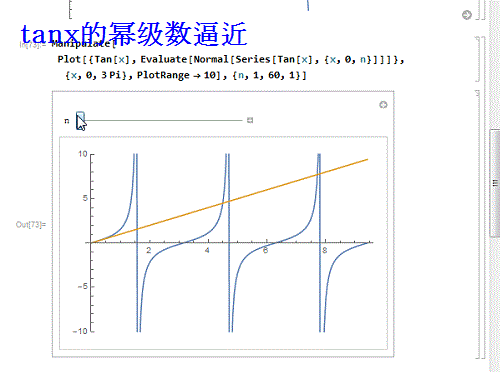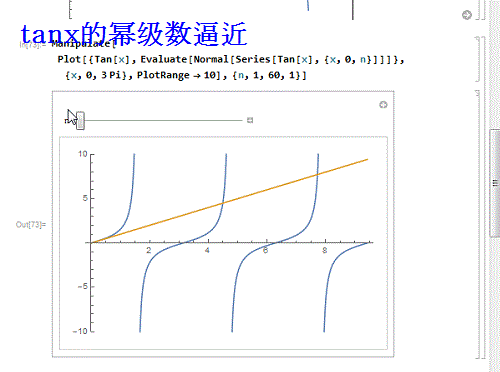
9/9

如果换一个不能处处收敛的呢？比如tanx：

Manipulate, Evaluate, {x，0, n}]]]}, {x, 0,

3 Pi}, PlotRange - 10], {n, 1, 60, 1}]

发现，只有在收敛区间内，幂级数才能逼近函数！

注意事项

Plot画图的时候，函数的幂级数展开式不能够带有余项，因此要用Normal处理一下。

还要“计算”一番，就是用Evaluate处理一下，至于为什么，我也不是很明白！

幂级数逼近函数，只发生在收敛区间内部！