结果为：a1-a

解题过程如下（因有专有公式，故只能截图）：

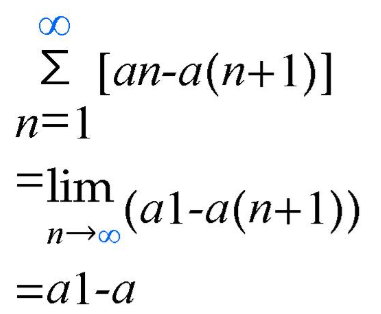
求收敛级数的方法：

函数级数是形如∑an(x-x0)^n的级数，称之为幂级数。它的结构简单 ，收敛域是一个以为中心的区间（不一定包括端点），并且在一定范围内具有类似多项式的性质，在收敛区间内能进行逐项微分和逐项积分等运算。

例如幂级数∑(2x)^n/x的收敛区间是，幂级数∑/(n^2)的收敛区间是，而幂级数∑(x^n)/(n!)在实数轴上收敛。

如果每一un≥0（或un≤0），则称∑un为正（或负）项级数，正项级数与负项级数统称为同号级数。正项级数收敛的充要条件是其部分和序列Sm 有上界。

例如∑1/n！收敛，因为：Sm=1+1/2!+1/3!+···+1/m!1+1+1/2+1/2+···+1/2^(m-1)3(2^3表示2的3次方)。

如果级数的每一项依赖于变量x,x 在某区间I内变化,即un=un(x),x∈I，则∑un(x)称为函数项级数,简称函数级数。

若x=x0使数项级数∑un(x0)收敛，就称x0为收敛点，由收敛点组成的集合称为收敛域，若对每一x∈I，级数∑un(x)都收敛，就称I为收敛区间。