信号处理过程中，经常需要对信号进行统计分析，包括对信号的时域分析和频域分析，进而更好的对信号特征进行提取，常用的统计信号处理的方法有：相关性与协方差，频谱分析，功率谱分析，现代谱分析，时频分析等方法，今天就这些统计信号处理的方法进行简单介绍：工具/原料more统计信号信号处理方法/步骤1/6分步阅读

相关性

MATLAB中xcorr函数用来计算自相关系数，其调用格式如下：

c=xcorr(x,y,maxlags,’option’);

c=xcorr(x);

=xcorr(x,y,maxlags,’option’);

其中x,y表示输入数据，c自相关系数，option计算自相关系的计算方法，可以有有偏计算，无偏计算，coeff，none等，maxlags设置计算范围，lags获取计算范围参数

示例：利用xcorr函数计算随机序列的自相关系数

编写对应的m文件如下:

x=randn(20,1);

subplot(1,3,1)

stem(x);

title(随机序列);

c=xcorr(x,20,coeff);%%默认得到计算范围%%

subplot(1,3,2)

stem(c);

title(默认范围的自相关系数);

=xcorr(x,20,coeff);%%c表示自相关系数，lags表示获取计算范围%%

subplot(1,3,3)

stem(lags,c1);

title(获取特定范围的自相关系数);

程序运行结果如下图：

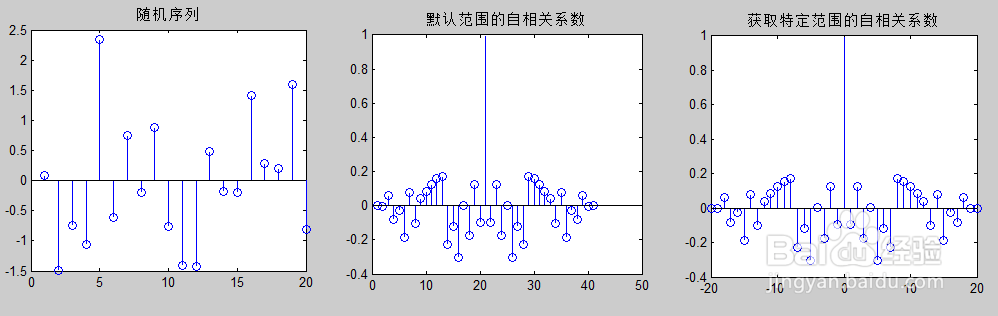2/6

协方差

MATLAB中xcov函数用来计算协方差系数，其调用格式如下：

c=xcov(x,y,maxlags,’option’);

=xcov(x,y,maxlags,’option’);

示例：利用xcov函数计算随机序列的协方差

编写对应的m文件如下：

x=randn(15,1);

subplot(1,3,1)

stem(x,r);

title(随机序列);

c=xcov(x,15,none);%%默认得到计算范围%%

subplot(1,3,2)

stem(c,r);

title(默认范围的协方差系数);

=xcov(x,15,coeff);%%c表示自相关系数，lags表示获取计算范围%%

subplot(1,3,3)

stem(lags,c1,r);

title(获取特定范围的协方差系数);

程序运行结果如下图：

3/6

频谱分析

Fft函数用于实现对时域信号的傅立叶变换，得到时域信号对应的频谱图，其调用格式如下

y=fft(x,N,dim);

其中x表示输入信号，y表示变换后信号，dim表示维数

示例：对一个含有30HZ和80HZ为主要成分的信号及进行傅立叶变换

编写对应的m文件如下：

Fs=2000;

T=1/Fs;

L=1000;

t=T*(0:L-1);

f1=100;

f2=200;

y=sin(2*pi*f1*t)+sin(2*pi*f2*t);

subplot(1,2,1)

plot(t(1:200),y(1:200),r);

title(时域波形图)

xlabel(时间/s);

ylabel(幅值);

y2=fft(y,1024);

f=Fs*(0:1023)/1024;

subplot(1,2,2)

plot(f(1:200),abs(y2(1:200))*2/1024,b);

title(频谱图);

xlabel(频率/Hz);

ylabel(幅值);

程序运行结果如下图：

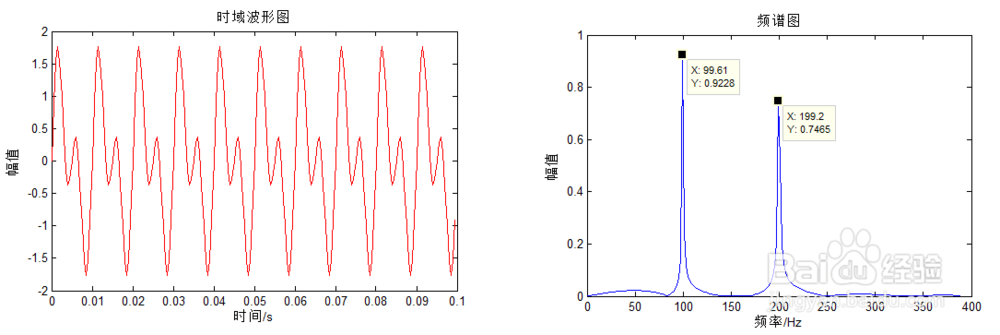4/6

功率谱估计，功率谱估计有三种，一是非参数方法包含周期图法，welch法，MTM法，二是参数方法，子空间法等，matlab中对应的函数如下：

spectrum.periodogram,periodogram用于周期图法，

spectrum.welch,pwelch,cpsd,tfesitamate,mscohere函数表示平均周期图法

Spectrum.yulear,pyulear函数表示以自相关分析为基础的AR方法（Yule-Walker法）

Spectrum.burg,pburg函数表示以线性预测为基础的AR方法（Burg法）

Spectrum.cov,pcov函数表示以最小前向预测误差为基础的AR方法（协方差法）

示例：使用不同的非参数方法对同一个信号进行功率谱分析

编写对应的m文件：

Fs=6000;

T=1/Fs;

L=1000;

t=T*(0:L-1);

f1=100;

f2=200;

y=2*sin(2*pi*f1*t)+2*sin(2*pi*f2*t);

subplot(2,3,1)

plot(t(1:200),y(1:200),r);

title(时域波形图);

xlabel(时间/s);

ylabel(幅值);

a1=spectrum.periodogram;%%周期图法%%

subplot(2,3,2)

psd(a1,y,Fs,Fs,NFFT,1024);

title(周期图法);

subplot(2,3,3)

a2=spectrum.periodogram(Hamming);%%加汉宁窗周期图法%%

psd(a2,y,Fs,Fs,NFFT,1024);

title(加汉宁窗周期图法);

a3=spectrum.periodogram(rectangular);%%加矩形窗周期图法%%

subplot(2,3,4)

psd(a3,y,Fs,Fs,NFFT,1024);

title(加矩形窗周期图法);

a4=spectrum.welch(rectangular,80,30);%%加矩形窗1平均周期法%%

subplot(2,3,5)

psd(a4,y,Fs,Fs,NFFT,1024);

title(加矩形窗1平均周期法);

a5=spectrum.welch(rectangular,70,50);%%加矩形窗2的平均周期法%%

subplot(2,3,6)

psd(a5,y,Fs,Fs,NFFT,1024);

title(加矩形窗2平均周期法);

程序运行结果如下图：

5/6

现代谱估计，现代谱估计方法即参数谱估计方法，对应函数在第4步已经介绍

示例：使用不同的现代谱估计对信号进行功率谱分析处理

编写对应的m文件如下：

load mtlb;

a1=spectrum.welch(hamming,256,60);%%加汉明窗平均周期法%%

a2=spectrum.yulear(14);%%以自相关分析为基础的AR方法%%

a3=spectrum.burg(14);%%以线性预测为基础的AR方法%%

a4=spectrum.cov(14);%%以最小前向预测误差为基础的AR方法%%

subplot(2,2,1)

psd(a1,mtlb,Fs,Fs,NFFT,1024);

title(加汉明窗平均周期法);

subplot(2,2,2)

psd(a2,mtlb,Fs,Fs,NFFT,1024);

title(以自相关分析为基础的AR方法);

subplot(2,2,3)

psd(a3,mtlb,Fs,Fs,NFFT,1024);

title(以线性预测为基础的AR方法)

subplot(2,2,4)

psd(a4,mtlb,Fs,Fs,NFFT,1024);

title(以最小前向预测误差为基础的AR方法);

程序运行结果如下图：

6/6

时频分析

对信号处理的过程中，有时候仅仅利用时域分析或者频域分析已经不能满足需要，需要同时利用时域和频率分析进行处理，于是时频联合分析应运而生，进行时域频域联合方法很多，最常用的是基于傅立叶变换的短时傅立叶变换，spectrogram函数用于实现短时傅立叶变换，其在matlab中调用格式如下：

S=spectrogram(X,window,noverlap,nfft,F,fs);

其中，X表示输入信号，window表示窗函数，noverlap表示重合点数，nfft表示变换的点数，F表示频率向量，fs表示采样频率，s表示变换后信号

示例：使用短时傅立叶变换对线性扫频信号进行谱估计

编写对应的m文件如下：

t=0:0.002:4;

x=chirp(t,0.1,150);

subplot(1,2,1)

plot(t,x);

title(原始信号);

xlabel(时间/s);

ylabel(幅值);

=spectrogram(x,256,250,256,1000);

subplot(1,2,2)

surf(T,F,10*log10(P),edgecolor,none);

xlabel(时间/s);

ylabel(HZ);

view(0,90);

colorbar;

title(短时傅立叶变换图像);

程序运行结果如下图：

统计信号信号处理