求函数f(x)的最值其实很简单，也有很多方法，比如，如果函数是一元二次函数的话，可以求其对称轴，对称轴与函数的交点即为函数的极值点，还比如一次性函数，只要定义域是闭区间或者是半闭区间，那么最值就是区间的闭端处取；如果函数是一元三次函数或者更复杂的函数，用普通的方法就很难求出结果了。那么怎么求复杂函数的最值呢，下面我就给大家介绍一下求这类问题的方法。工具/原料more纸笔方法/步骤1/7分步阅读

先求其导函数。比如，f(x)=x^3+3x^2+3x+3,用导函数的方法求就是：（设g（x)是fx的导函数，gx=3x^2+6x+3;

2/7

令导函数等于0，求解对应的方程。令gx=0，可得x=-1;

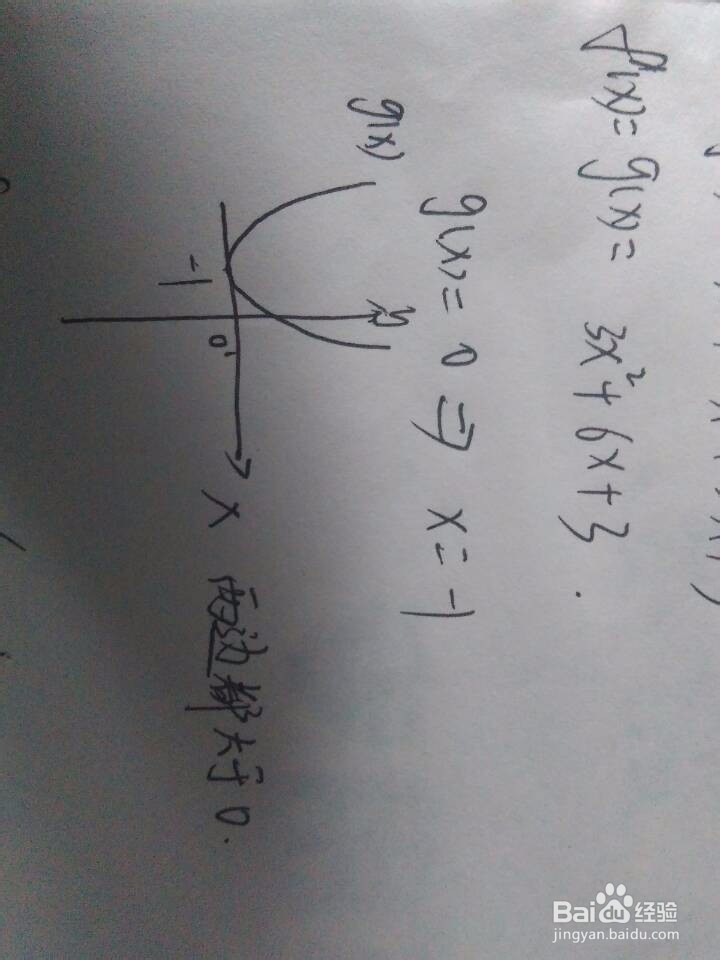3/7

根据导函数的函数图像特征来判断该点是极大值点还是极小值点，或者是既不是极大值点也不是极小值点。根据gx的图像特征可知，在x=1这一点的左边gx是大于0的，右边gx也是大于0的，根据“导函数大于0，函数是递增的”这一性质，可知fx在定义域内递增，因此fx没有极值点，于是更没有最值点。

4/7

再举一个例子。写到这个步骤时，突然发现这个函数缺少一般性，不能向读者展示求复杂函数的一般方法。再举一个函数吧，fx=(1/3)*(x^3)+(5/2)*(x^2)+6x+7,（定义域是【-7，-1】）这个函数，其导数是x^2+5x+6,令该导数等于0，即求x^2+5x+6=0这个方程，解得x=-2或x=-3；

5/7

然后画出x^2+5x+6这个函数的图像。可以发现，在x=-2的右侧，还有x=-3的左侧，导函数都是大于0的，而在-2和-3之间，导函数是小于0的。根据性质有，fx在x-3或x-2时是递增的，而在-3和-2之间是递减的。

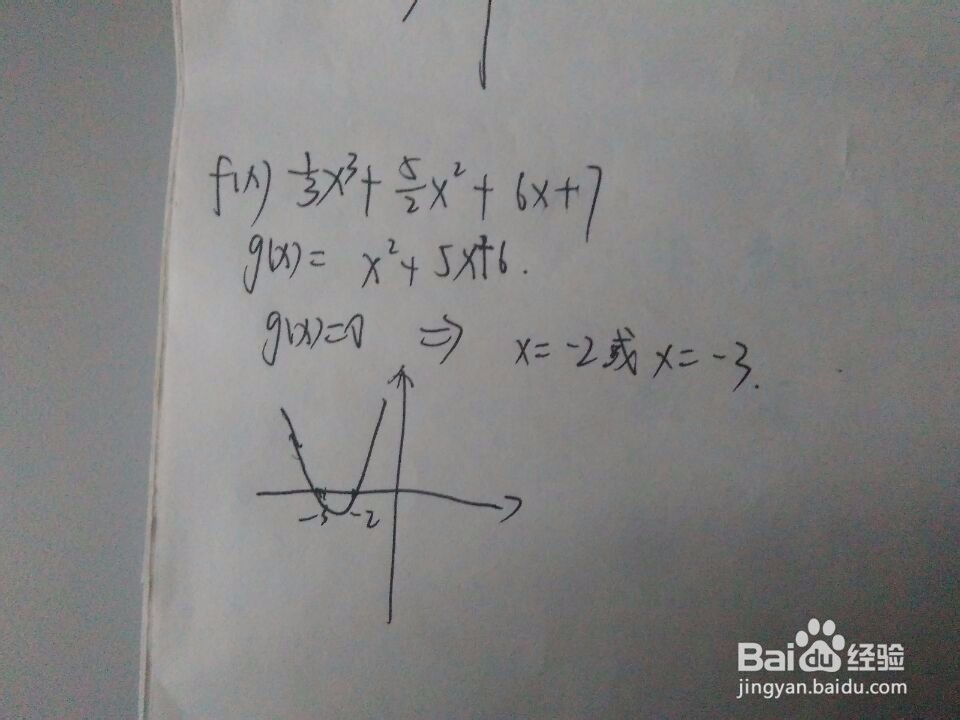6/7

根据函数图像可知-3是极大值点，-2是极小值点。

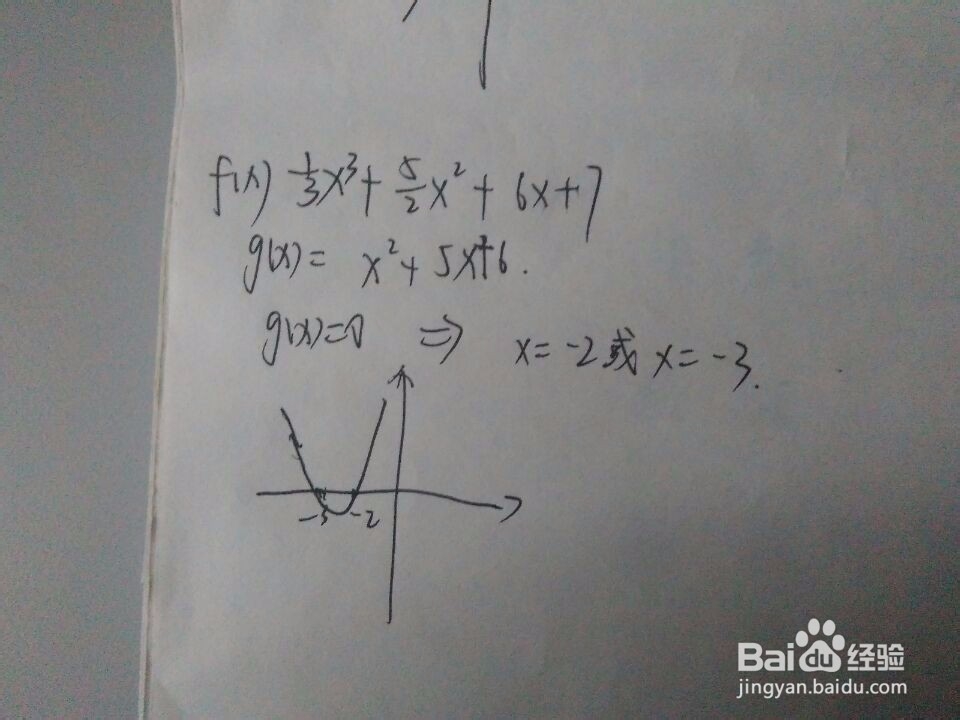7/7

再来看看定义域，是【-7，-1】，两边都是闭的，于是将两端的值和极大极小值进行比较，即分别求得f(-7),f(-1),f(-3),f(-2)的值，进行比较，最小的那一个即为最小值，最大的那一个就是最大值。

注意事项

求复杂函数的最值，关键就是求其导函数。因此要熟练的掌握导函数的求法。

图像一点要画好，否则会导致误判。