订阅【抽象代数】给定集合生成的群的Cayley图
来源：网络收集 点击： 时间：2024-02-21如果集合S含有三个元素：
{{{0, 0, 0, 1}, {0, 1, 0, 0}, {0, 0, 1, 0}, {1, 0, 0, 0}},
{{0, 0, 1, 0}, {0, 0, 0, 1}, {1, 0, 0, 0}, {0, 1, 0, 0}},
{{0, 1, 0, 0}, {1, 0, 0, 0}, {0, 0, 0, 1}, {0, 0, 1, 0}}}
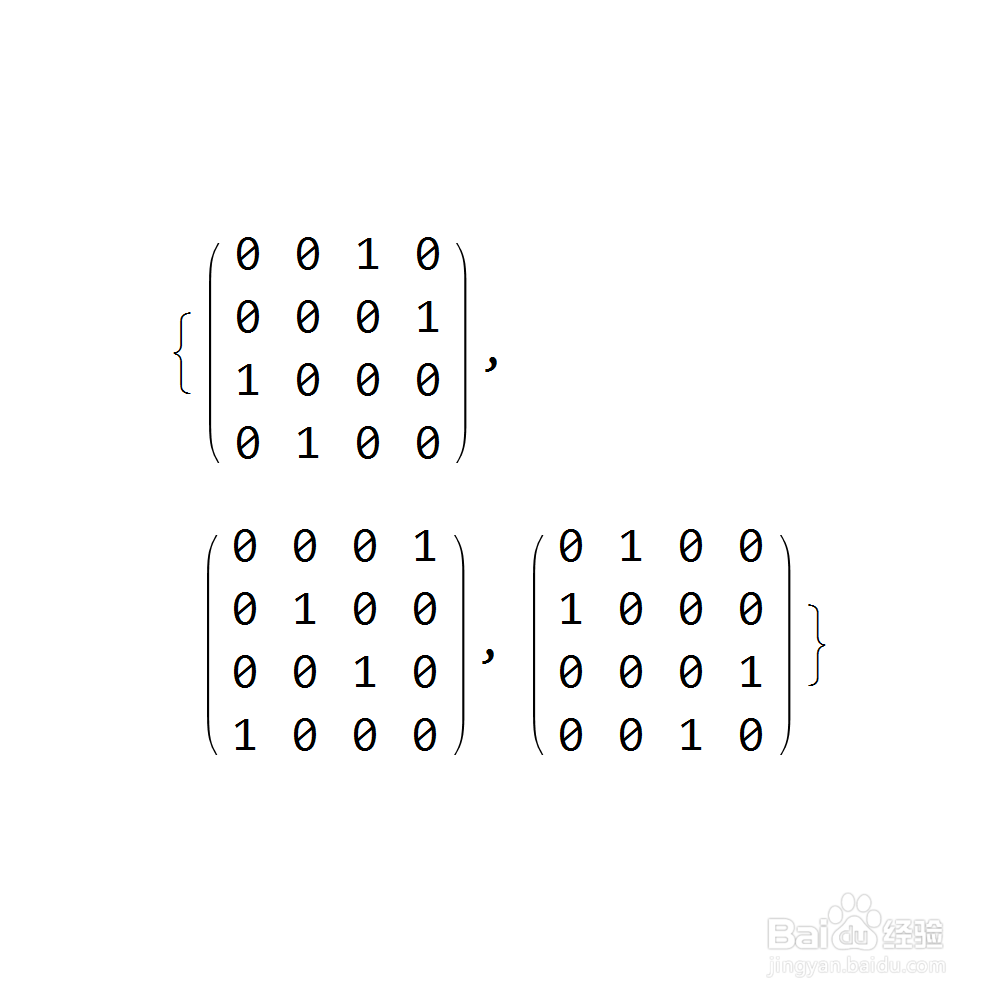2/8那么集合S就可以生成一个八阶群G，根据S来绘制G的Cayley图，如下：
3/8S={{{0, 0, 0, 1}, {0, 0, 1, 0}, {0, 1, 0, 0}, {1, 0, 0, 0}},
{{0, 0, 0, 1}, {1, 0, 0, 0}, {0, 1, 0, 0}, {0, 0, 1, 0}}}
生成的也是八阶群，但Cayley图与上图不太一样。
4/8S={{{0, 0, 0, 1}, {0, 1, 0, 0}, {0, 0, 1, 0}, {1, 0, 0, 0}},
{{0, 1, 0, 0}, {0, 0, 0, 1}, {0, 0, 1, 0}, {1, 0, 0, 0}}}
S的元素包括二阶元素一个、三阶元素一个，此时生成的群是六阶群。
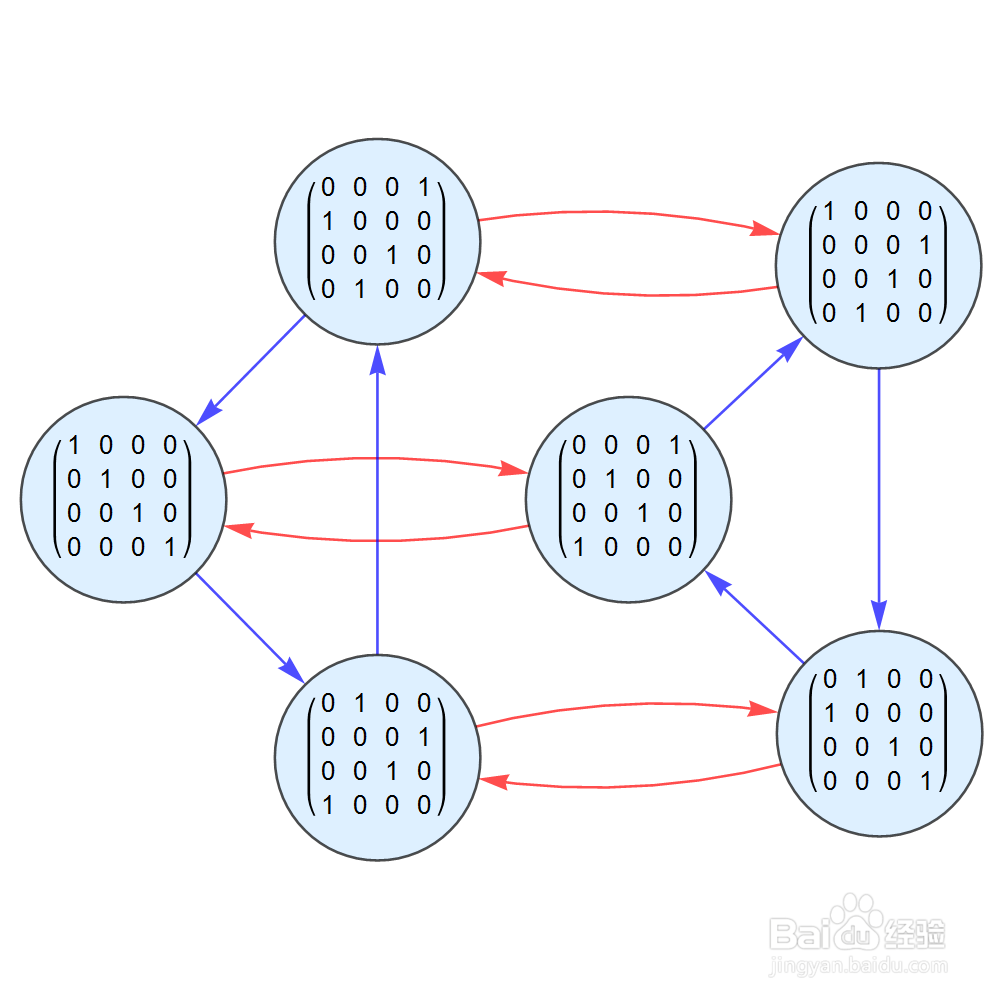5/8S={{{0, 0, 0, 1}, {0, 0, 1, 0}, {0, 1, 0, 0}, {1, 0, 0, 0}},
{{0, 0, 0, 1}, {0, 1, 0, 0}, {1, 0, 0, 0}, {0, 0, 1, 0}}}
S的元素包括二阶元素一个、三阶元素一个，此时生成的群是十二阶群。
它是s4的唯一的二阶子群，此时的Cayley图如下：
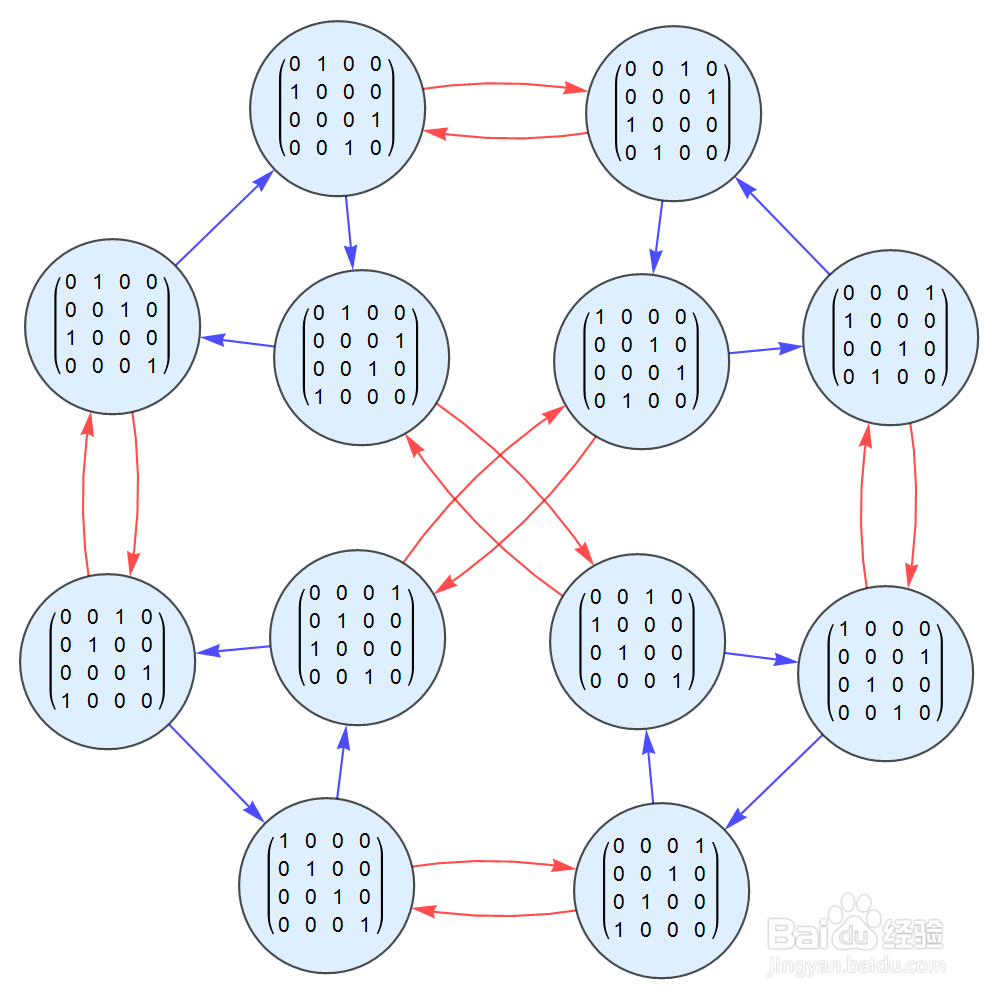6/8如果S等于：
{{{0, 0, 0, 1}, {0, 1, 0, 0}, {0, 0, 1, 0}, {1, 0, 0, 0}},
{{0, 0, 1, 0}, {0, 0, 0, 1}, {1, 0, 0, 0}, {0, 1, 0, 0}},
{{0, 0, 1, 0}, {0, 1, 0, 0}, {1, 0, 0, 0}, {0, 0, 0, 1}}}
G是24阶群，恰好就是s4。但是因为几何S有3个元素，所以Cayley也有三种不同颜色的箭头。
因为S中的元素都是二阶的，因此Cayley图中只有二阶轨道。
这与下文中的s4的Cayley图不一样。
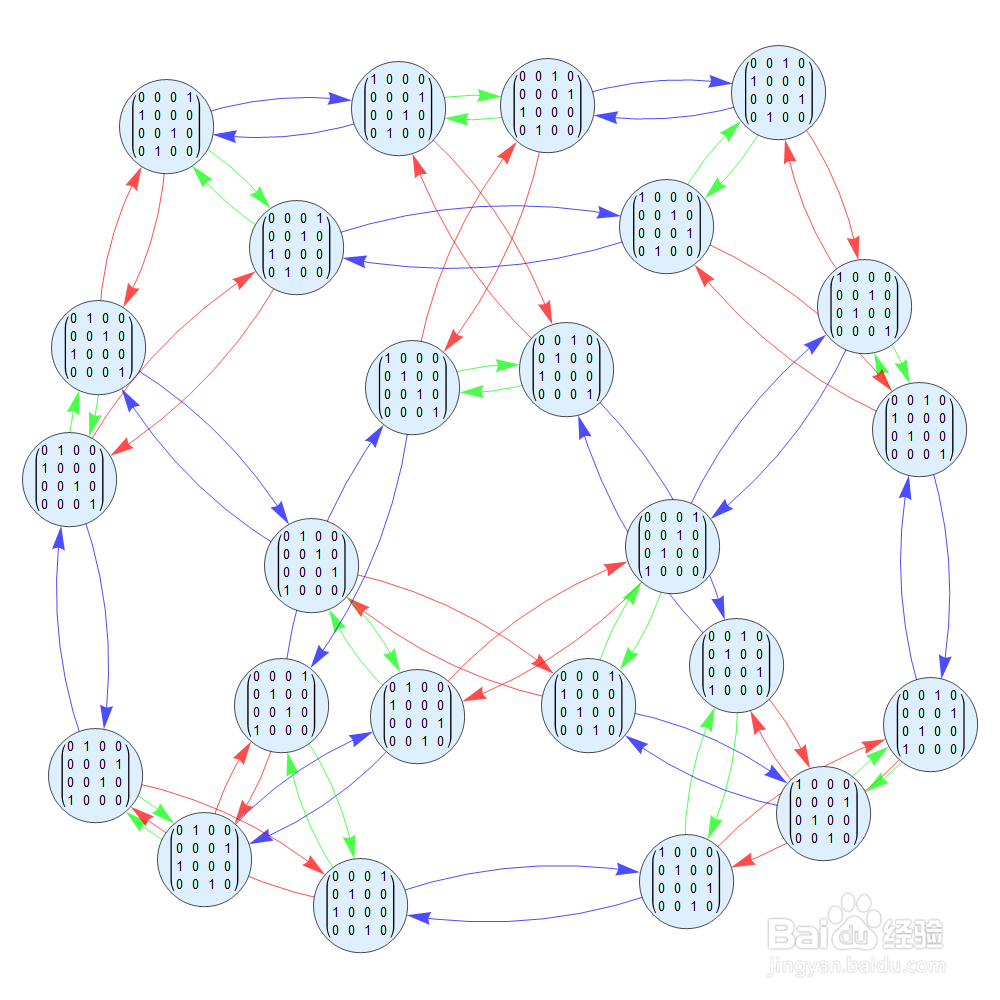7/8S={{{0, 0, 0, 1}, {0, 1, 0, 0}, {0, 0, 1, 0}, {1, 0, 0, 0}},
{{0, 1, 0, 0}, {0, 0, 1, 0}, {0, 0, 0, 1}, {1, 0, 0, 0}}}
生成s4，但S的两个元素分别是二阶和四阶的，因此Cayley图中的轨道，分别是二阶和四阶的。
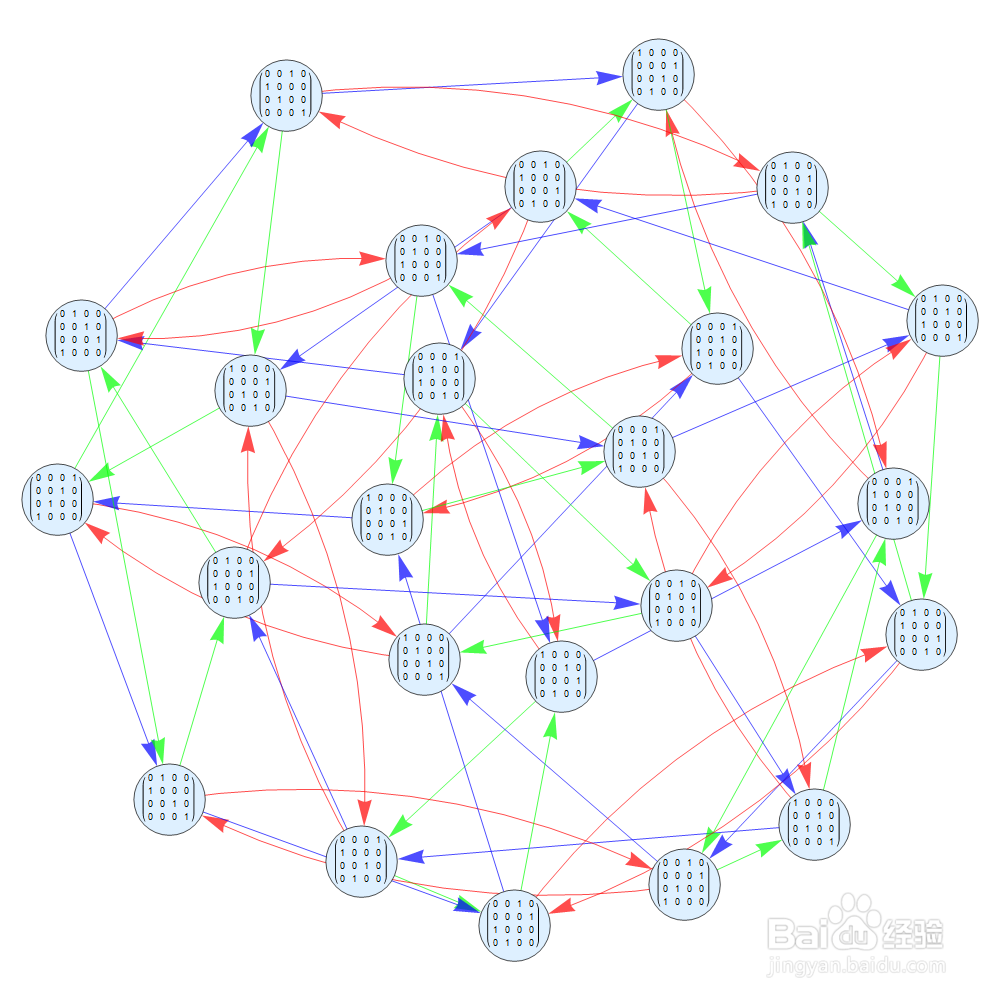
8/8S={{{0, 0, 0, 1}, {0, 0, 1, 0}, {0, 1, 0, 0}, {1, 0, 0, 0}},
{{0, 0, 0, 1}, {0, 0, 1, 0}, {1, 0, 0, 0}, {0, 1, 0, 0}},
{{0, 0, 0, 1}, {0, 1, 0, 0}, {1, 0, 0, 0}, {0, 0, 1, 0}}}
S中二阶、三阶、四阶元素各一个，请读者在Cayley图中找出所有的二阶、三阶、四阶轨道。
注意事项对于确定的有限群，如果选择的生成元集合不同，得到的Cayley图也不一样。因此，Cayley图不同的群，有可能同构。
版权声明：
1、本文系转载，版权归原作者所有，旨在传递信息，不代表看本站的观点和立场。
2、本站仅提供信息发布平台，不承担相关法律责任。
3、若侵犯您的版权或隐私，请联系本站管理员删除。
4、文章链接：http://www.1haoku.cn/art_95821.html
