高中数学一对一辅导数列的概念与简单表示法|附解题技巧数列在高中数学不算难题，但是很多同学对数列掌握不好，下面肖老师给大家介绍关于高中数学数列中，如何去解题掌握好解题思路其实学好数列并不难。老师今天讲解今天给同学讲解数列的概念与简单表示法习题解答过程。方法/步骤1/9分步阅读

由an与Sn的关系求通项公式an：an与Sn关系的应用是高考的常考内容，且多出现在选择题或填空题中，有时也出现在解答题的已知条件中，难度较小．

高考对an与Sn关系的考查常有以下两个命题角度：

(1)由Sn求通项公式an；

(2)利用an与Sn的关系求Sn.

2/9

(1)已知数列{an}的前n项和Sn＝3n2－2n＋1，则其通项公式为________．

(2)(2015·高考全国卷Ⅱ)设Sn是数列{an}的前n项和，且a1＝－1，an＋1＝SnSn＋1，则Sn＝________．

3/9

规律方法：已知Sn求an的三个步骤

(1)先利用a1＝S1求出a1.

(2)用n－1(n≥2)替换Sn中的n得到一个新的关系，利用an＝Sn－Sn－1(n≥2)便可求出当n≥2时an的表达式．

(3)对n＝1时的结果进行检验，看是否符合n≥2时an的表达式，如果符合，则可以把数列的通项公式合写；如果不符合，则应该分n＝1与n≥2两段来写．

4/9

角度一由Sn求通项公式an

1．已知数列{an}满足a1＋2a2＋3a3＋4a4＋…＋nan＝3n2－2n＋1，求an.

5/9

角度二利用an与Sn的关系求Sn

2．已知数列{an}的前n项和为Sn，a1＝1，Sn＝2an＋1，

则Sn＝()

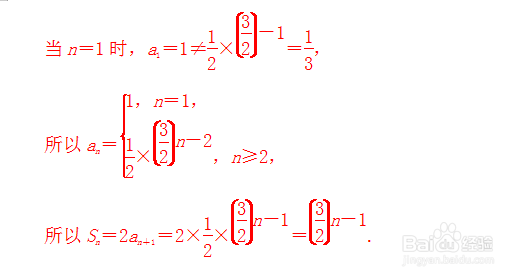
6/9

由递推关系求数列的通项公式

分别求出满足下列条件的数列的通项公式．

(1)a1＝0，an＋1＝an＋(2n－1)(n∈N*)；

(2)a1＝1，an＝n－1(n)an－1(n≥2，n∈N*)；

(3)a1＝1，an＋1＝3an＋2(n∈N*)．

7/9

数列的性质

(1)已知数列{an}的通项公式为an＝11－2n(4)(n∈N*)，则满足an＋1＜an的n的取值为()

A．3 B．4

C．5 D．6

(2)(2017·昆明市两区七校调研)在数列{an}中，a1＝5，(an＋1－2)(an－2)＝3(n∈N*)，则该数列的前2 018项的和是________．

8/9

(1)解决数列单调性问题的三种方法

①作差比较法，根据an＋1－an的符号判断数列{an}是递增数列、递减数列还是常数列．

②作商比较法，根据an(an＋1)(an＞0或an＜0)与1的大小关系进行判断．

③结合相应函数的图象直观判断．

(2)解决数列周期性问题的方法

先根据已知条件求出数列的前几项，确定数列的周期，再根据周期性求值．

(3)数列的最值可以利用数列的单调性或求函数最值的思想求解．

9/9

1．设函数f(x)＝ax－6（x＞7），(（3－a）x－3（x≤7），)

数列{an}满足an＝f(n)，n∈N*，且数列{an}是递增数列，则实数a的取值范围是()

高中数学高考数学