利用MATLAB求单自由度振动系统的动力响应
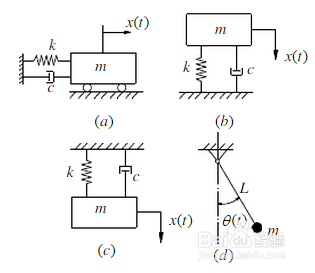
来源:网络收集 点击: 时间:2024-03-01问题:一单自由度系统,固有频率wn=1,初始条件,y0=1,v0=5,系统的阻尼大小可变,讨论系统在过阻尼、小阻尼和无阻尼情况下的自由振动。
 2/5
2/5分析1:当系统的阻尼为0,称为无阻尼,此时系统的振动效应为:
 3/5
3/5分析2:当系统的阻尼比介于0~1之间,称为小阻尼,此时系统的振动效应为:
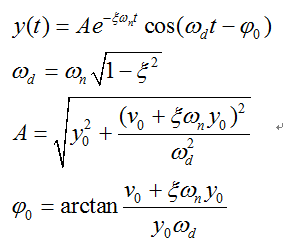 4/5
4/5分析3:当系统的阻尼比大于1,称为过阻尼,此时系统的振动效应为:
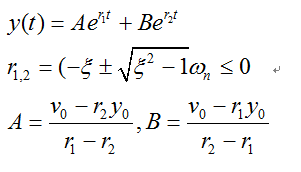 5/5
5/5MATLAB计算
假设:过阻尼时阻尼比为1.5,过阻尼时阻尼比为0.5,无阻尼时阻尼比为0,则
clear
t=0:0.01:20;
wn=5;y0=1;v0=5;
%%阻尼比znb=0时,计算无阻尼响应
znb=0;
A1=sqrt(y0^2+(v0/wn)^2);
phi1=atan(v0/(y0*wn));
y1=A1*cos(wn*t-phi1);
subplot(3,1,1);
plot(t,y1);
ylabel({\ity}_1);
grid on
%%阻尼比znb=0.1时,计算小阻尼响应
znb=0.1;
wd=wn*sqrt(1-znb^2);
A2=sqrt(y0^2+(v0+znb*wn*y0)^2/wn^2);
phi2=atan(v0+znb*wn*y0)/(y0*wd);
y2=A2*exp(-znb*wn*t)*diag(cos(wd*t-phi2));%使用diag函数生成对角阵满足矩阵乘法运算。
subplot(3,1,2);
plot(t,y2);
ylabel({\ity}_2);
grid on
%%阻尼比znb=1.5时,计算过阻尼响应
znb=1.5;
r1=(-znb+sqrt(znb^2-1))*wn;
r2=(-znb-sqrt(znb^2-1))*wn;
A=(v0-r2*y0)/(r1-r2);
B=(v0-r1*y0)/(r2-r1);
y3=A*exp(r1*t)+B*exp(r2*t);
subplot(3,1,3);
plot(t,y3);
ylabel({\ity}_3);
xlabel({\itt});
grid on



版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_191168.html
 订阅
订阅