对正定矩阵进行Cholesky分解(Mathematica)
来源:网络收集 点击: 时间:2024-03-19【导读】:
给定一个方阵,Mathematica可以快速地对这个矩阵进行Cholesky分解。工具/原料more电脑Mathematica方法/步骤1/7分步阅读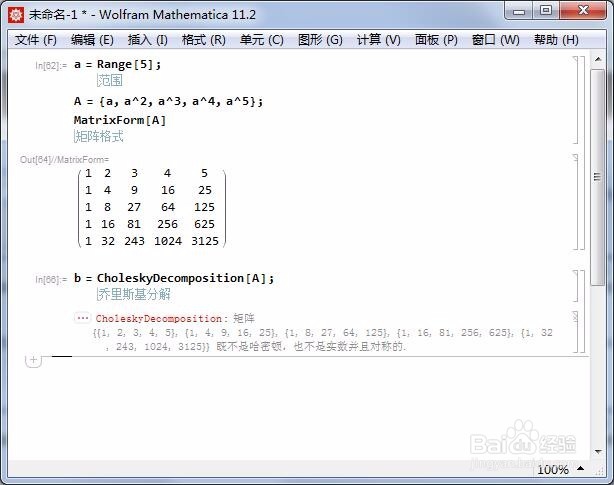 2/7
2/7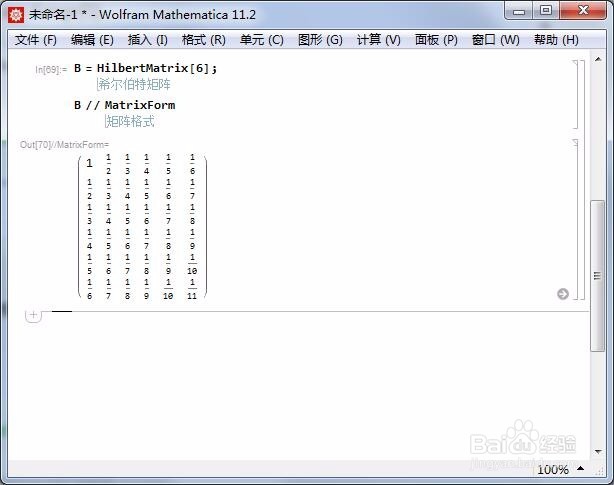 3/7
3/7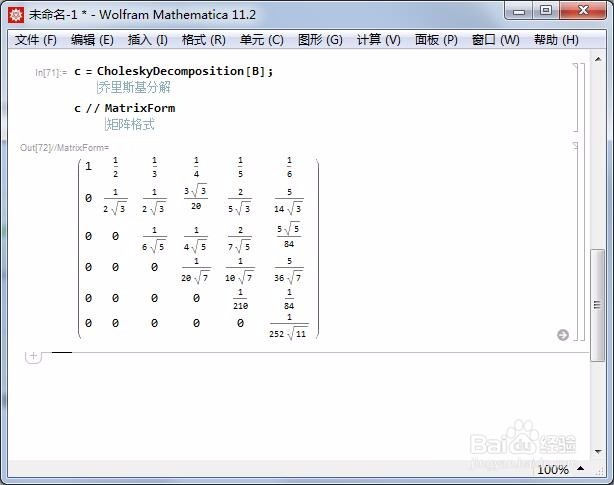 4/7
4/7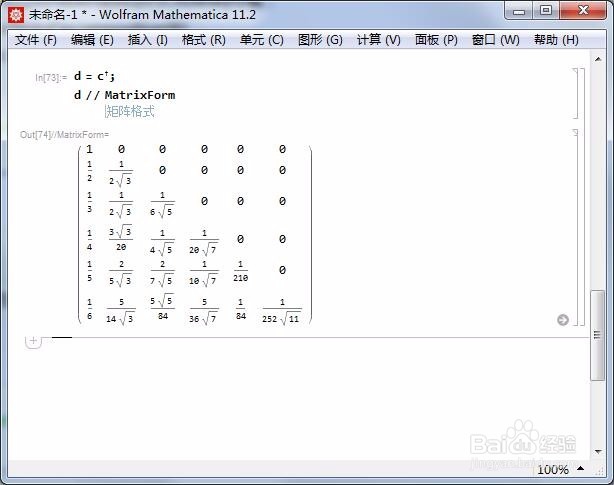 5/7
5/7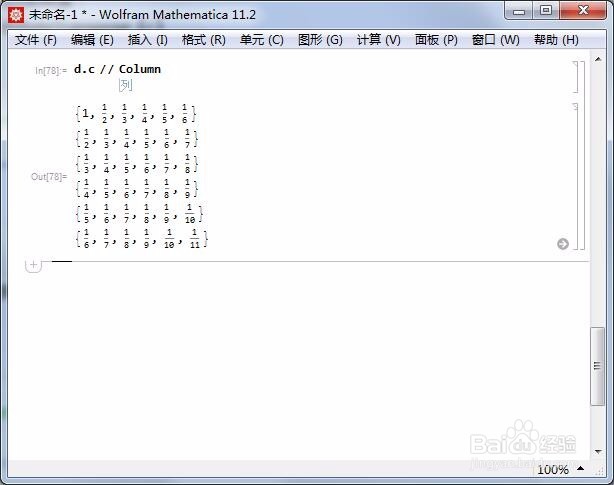 6/7
6/7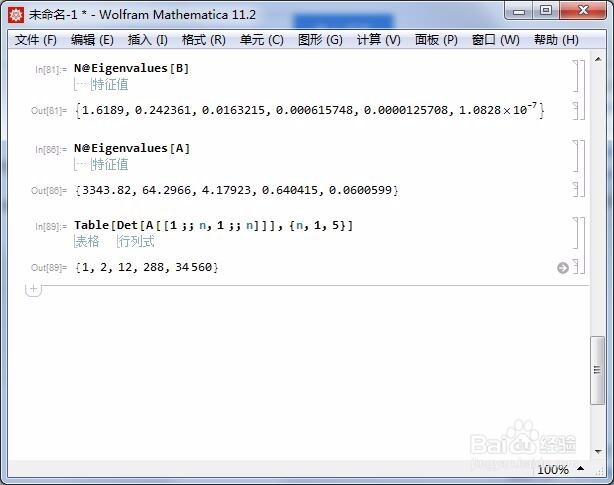 7/7
7/7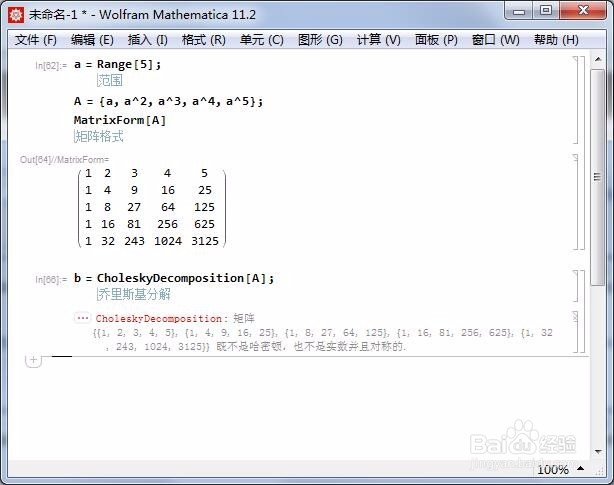 注意事项
注意事项
A = {a, a^2, a^3, a^4, a^5};
其中,a = Range;
A不能进行Cholesky分解:
b = CholeskyDecomposition;
 2/7
2/7Hilbert矩阵都是正定矩阵:
B = HilbertMatrix;
 3/7
3/7因此,可以对Hilbert矩阵进行Cholesky分解:
c = CholeskyDecomposition;
这里的c是一个上对角矩阵。
 4/7
4/7计算c的共轭转置:
d=ConjugateTranspose【c】
 5/7
5/7d与c的矩阵积,就是B。
 6/7
6/7判断矩阵是否正定矩阵,可以查看矩阵的特征值是否全是正数:
N@Eigenvalues
还可以检测矩阵的所有主子式的行列式是否都是正数:
Table]], {n, 1, 5}]
两种方法都证明了A是正定矩阵。
 7/7
7/7可是为什么A不能进行Cholesky分解?
 注意事项
注意事项留下了一个疑问,为什么正定矩阵A不能进行Cholesky分解?
MATHEMATICACHOLESKY分解抽象代数正定矩阵版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_359246.html
上一篇:微信视频聊天看不到对方怎么办
下一篇:美食教学之紫薯芋泥蜂蜜牛奶!
 订阅
订阅