MATLAB提供函数interpft(x,n)进行一维快速傅里叶(Fourier)插值，interpft(x,n)的使用说明为：该函数使用傅里叶变换把输入数据x变换到频域，然后用更多的点（n点）傅里叶逆变换到时域。一维快速傅里叶(Fourier)插值是对数据进行增采样。工具/原料moreMATLABinterpft方法/步骤1/5分步阅读

第一，演示一维快速傅里叶插值。启动MATLAB，新建脚本（Ctrl+N），输入如下代码：

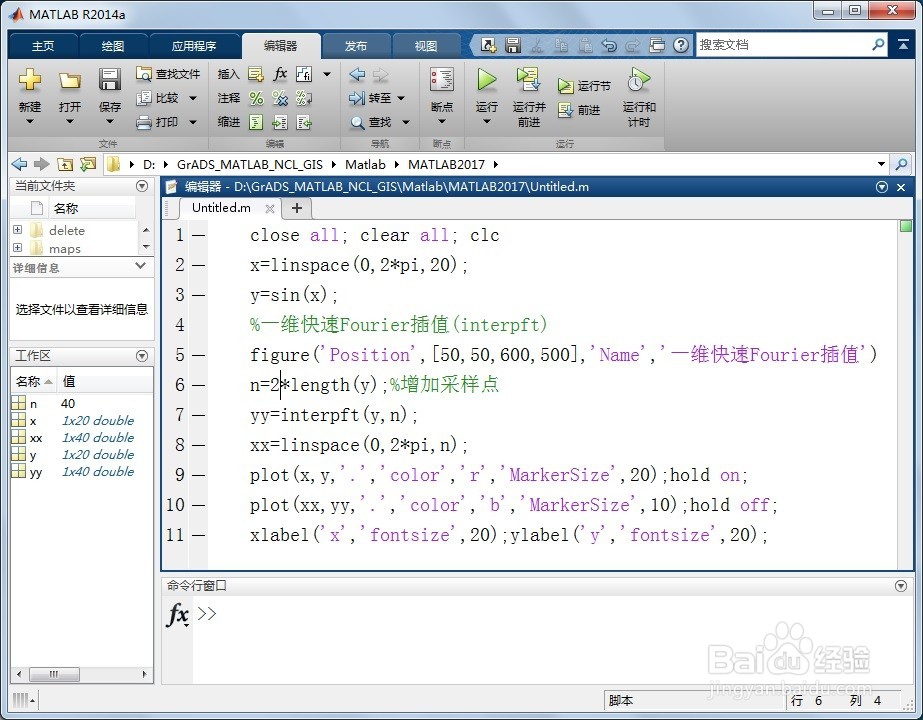
close all; clear all; clc

x=linspace(0,2*pi,20);

y=sin(x);

%一维快速Fourier插值(interpft)

figure(Position,,Name,一维快速Fourier插值)

n=2*length(y);%增加采样点

yy=interpft(y,n);

xx=linspace(0,2*pi,n);

plot(x,y,.,color,r,MarkerSize,20);hold on;

plot(xx,yy,.,color,b,MarkerSize,10);hold off;

xlabel(x,fontsize,20);ylabel(y,fontsize,20);

其中n=2*length(y)是对增加采样点为2倍的输入数据大小。

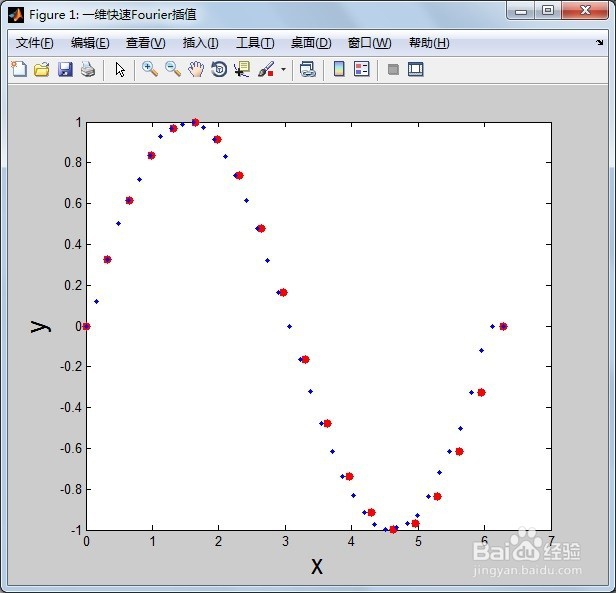
2/5

第二，保存和运行上述脚本，得到如下图形，红点为一元函数y=sin(x)的原始值，蓝点为一维快速傅里叶插值后的值，蓝点的数量是红点的2倍。

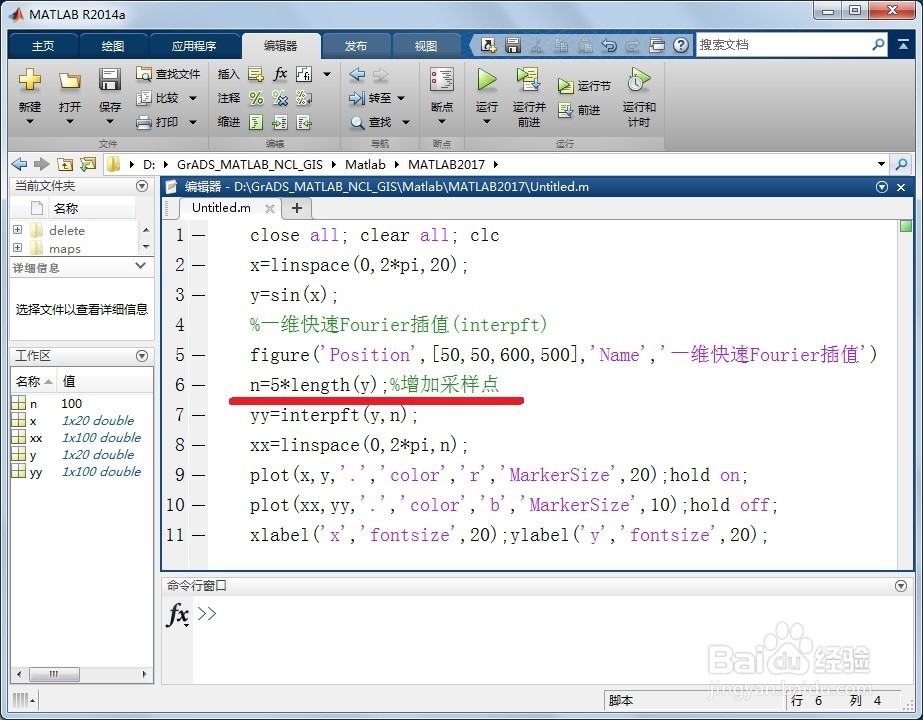
3/5

第三，第一步interpft(y,n)中n点傅里叶逆变换到时域，而n的大小为2倍的length(y)，我们现在改为n=5*length(y)，看一下增加5倍采样点后的插值结果。

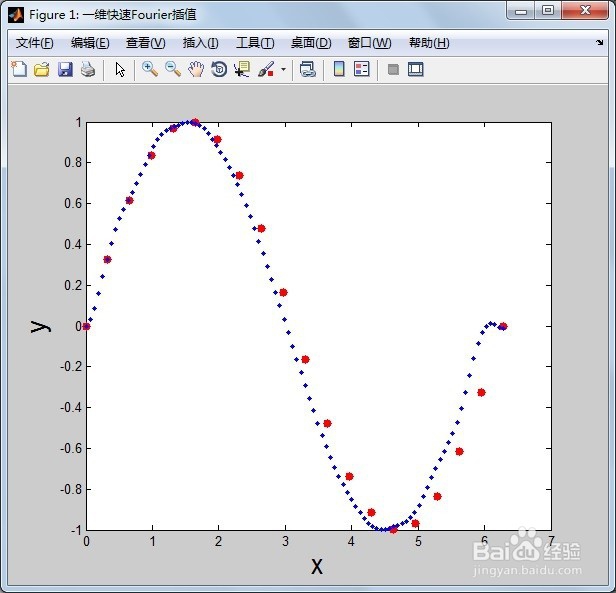
4/5

第四，保存和运行上述脚本，得到增加5倍采样点后的插值图形，红点为一元函数y=sin(x)的原始值，蓝点为一维快速傅里叶插值后的值，蓝点的数量是红点的5倍。

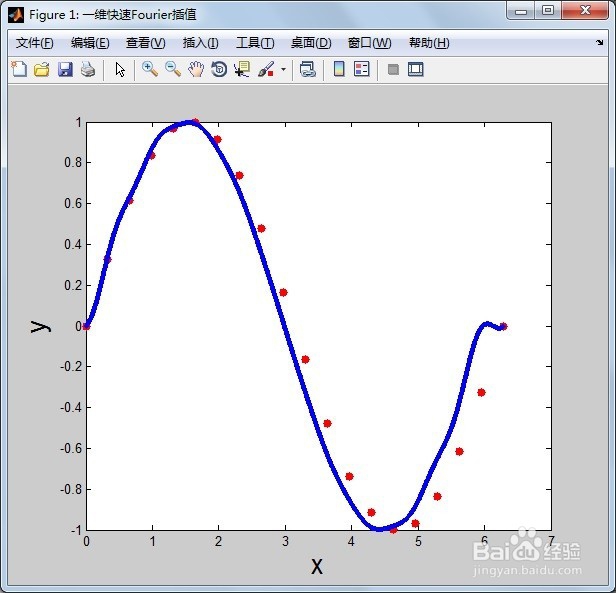
5/5

第五，最后我们看一下n=100*length(y)时一维快速傅里叶插值后的结果，如下图，蓝点密集成一条正弦曲线。

注意事项

一维快速傅里叶插值interpft(x,n)中，n要大于x的长度，即n大于length(x)

MATLABINTERPFTFOURIER频域时域