当数学规划模型中有多个目标函数时，称为多目标规划（multiple objective progamming，MOP）模型. 模型形式如下:在很多实际问题中，衡量一个方案的好坏往往难以用一个指标来判断，而需要用多个目标来比较. 因此有许多学者致力于这方面的研究. 多目标最优化思想最早是在1896 年由法国经济学家V. 帕雷托提出来的. 之后，J. 冯·诺依曼、H. W. 库恩、A. W. 塔克尔、A. M. 日夫里翁等数学家做了深入的探讨. 但是至今关于多目标最优解尚未有一个完全令人满意的定义，所以多目标规划仍处于发展阶段.求解多目标规划的方法大体上有以下几种：一种是化多为少的方法，即把多目标化为比较容易求解的单目标或双目标，如线性加权法、理想点法等；另一种叫分层序列法，即把目标按其重要性给出一个序列，每次都在前一目标最优解集内求下一个目标最优解，直到求出共同的最优解. 对多目标的线性规划除以上方法外还可以适当修正单纯形法来求解；还有一种称为层次分析法，是由美国运筹学家沙旦于20 世纪70 年代提出的，这是一种定性与定量相结合的多目标决策与分析方法，对于目标结构复杂且缺乏必要的数据的情况更为实用.工具/原料moreWindows 10家庭中文版Lingo 17 X64商业版实例 1/7分步阅读

联欢会食物采购

问题: 某班级要开元旦联欢会，需要采购瓜子、水果和糖果. 瓜子每千克8 元，水果每千克5 元，糖果每千克12 元. 同学们对三种不同食物喜爱程度不同，而且数量越大满意程度越高. 可以简化为整个班级因为采购了某种食品而提高的满意度与该种食品数量成正比，比例系数是三种食品之间比较而得到的相对喜爱程度. 糖果作为比较参照物，其喜爱程度设为1，瓜子相对于糖果喜爱程度为0.5，对水果的喜爱程度为0.4. 为保证基本需要，瓜子至少要买10kg，水果至少买5kg，糖果至少买2kg. 班级共有40 人，每人最多收20 元班费. 如何采购可以使花钱最少而满意度最高？

问题分析 这个问题有两个优化目标，一个是花钱最少，一个是满意度最高，显然是互相矛盾的. 如何权衡两个方面的要求是解决问题的关键.

模型建立

决策变量：三种食物采购量，设为瓜子x1 kg、水果x2 kg、糖果x3 kg .

目标函数：两个目标分别为：

采购三种食物花钱总数z1=8x1+5x2+12x3；

班级对采购结果的满意度z2 =0.5x1+0.4x2 +x3 .

约束条件：总费用不能超过800 元；瓜子至少要买10 kg，水果至少买5 kg，糖果至少买2 kg.

建立多目标规划模型：

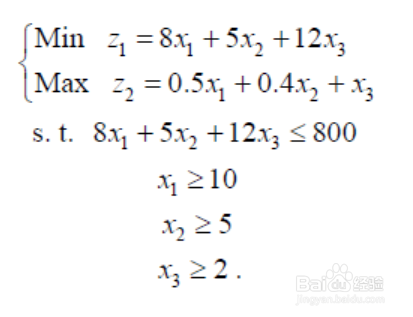2/7

模型求解

两个目标函数一个要最大，一个要最小，可以变成都求最大或者都求最小. 例如，下图所示:

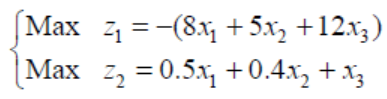3/7

多目标规划求解主要有加权系数法和分层序列法，下面采用加权系数法求解. 加权系数法是给两个目标设定不同的权重，然后做线性组合构成一个目标函数. 即令z=az1+bz2，其中a =0，b= 0，且a +b =1. 从而化多目标规划模型为单目标规划模型。

权重系数a 和b 反映两个目标之间相对的重要程度，可以通过专家根据经验或者大家协商等方式产生. 注意，满意度与总花费虽然都是三种食品数量的线性函数，但是因为系数相差10 多倍所以函数值相差10 多倍. 加权组合时首先应该使两个目标在数量级上相同，数值大小上比较接近，这样才能体现权重的含义. 本例可令z= a*z1 +b *14*z2 ，得到单目标规划模型如下：

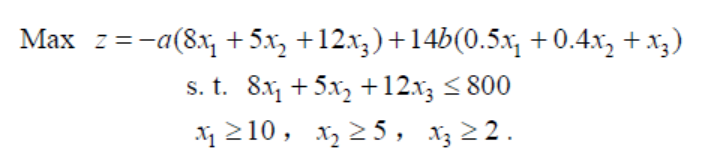4/7

使用LINGO17求解，输入代码如下：

model:

max=-a*(8*x1+5*x2+12*x3)+b*14*(0.5*x1+0.4*x2+x3);

8*x1+5*x2+12*x3=800;

x1=10;

x2=5;

x3=2;

data:

a=0.8;

b=0.2;

enddata

end

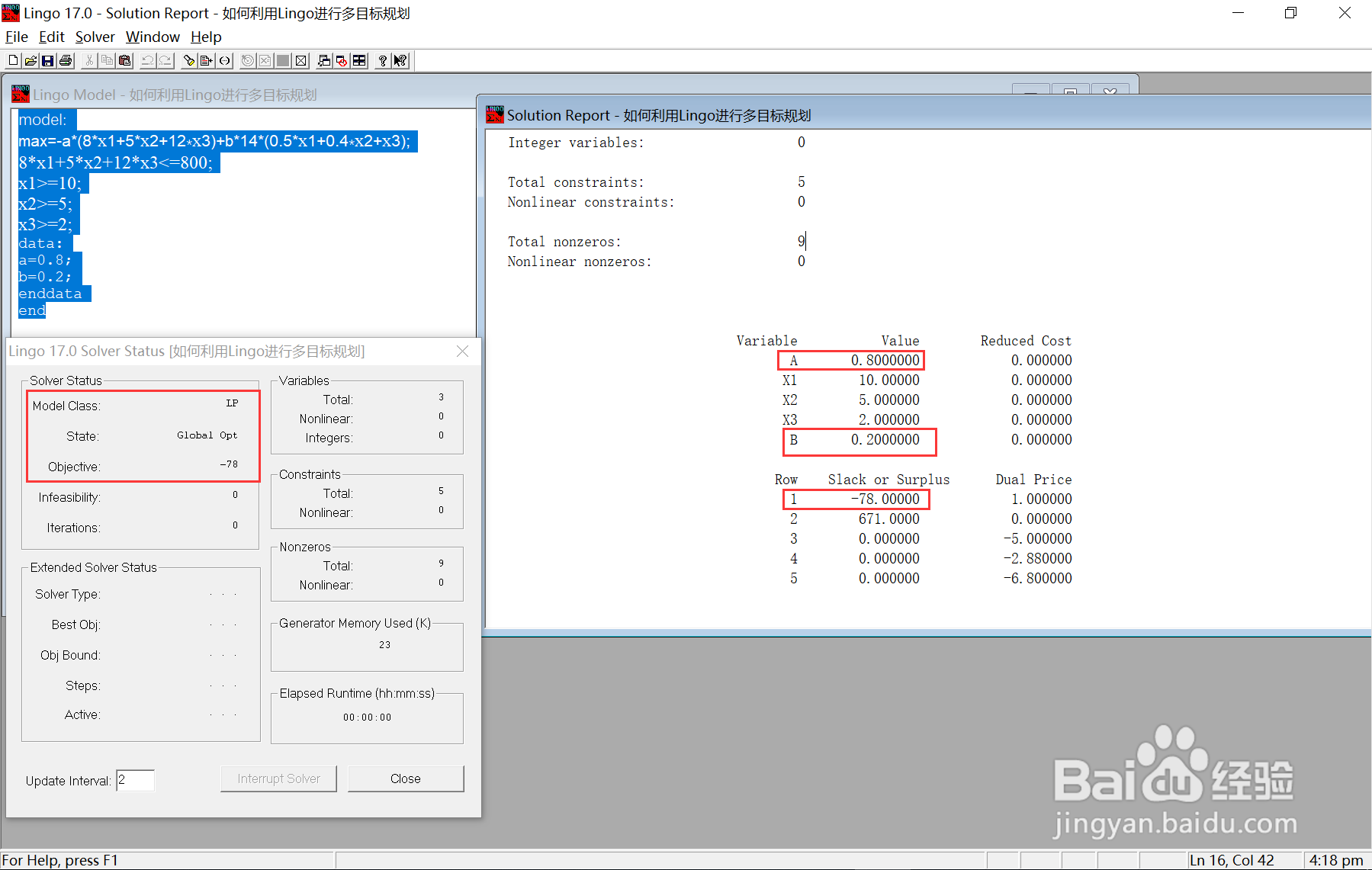5/7

上图结果显示，当更倾向于花钱少时只购买最低数量的食物是最佳选择。

6/7

若令a = 0.2 ，b= 0.8，即倾向于对食物满意度高时，显然，增加购买糖果可以在少花钱的情况下最大程度提高满意度.如下图所示:

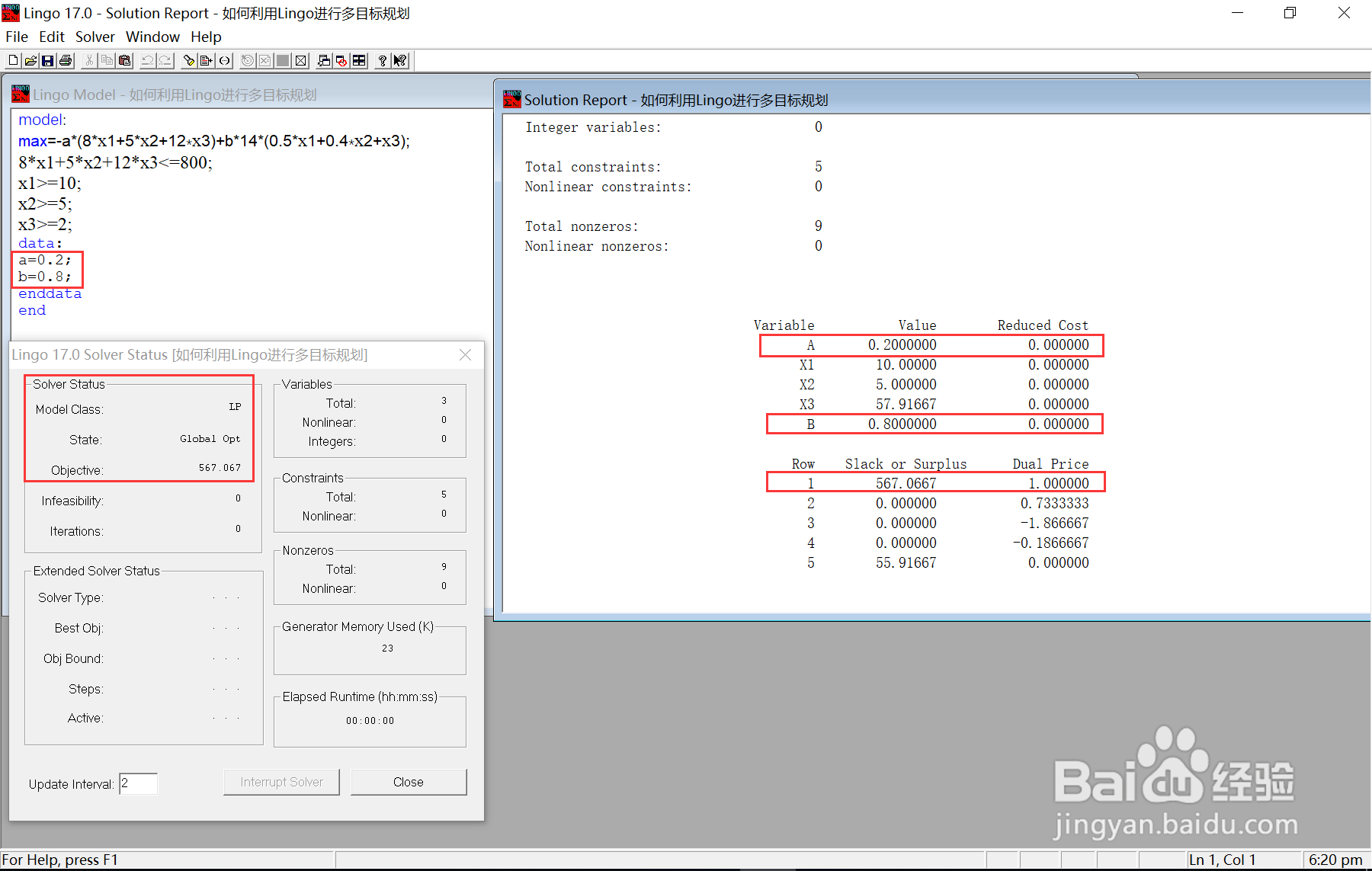7/7

本例讨论了多目标函数规划问题的建模及求解方法. 求解基本思想是通过加权组

合形成一个新的目标，从而化为单目标规划. 需要注意的是，不同的目标函数量纲可能不同，导致在数值大小上差异很大，在加权组合时需要首先处理这个问题。

注意事项

如果对于不同版本的Lingo,其求解操作过程可能有细微的不同,请您自行加以调整。

师者，所以传道受业解惑也。人非生而知之者，孰能无惑？惑而不从师，其为惑也，终不解矣。如对您有帮助，请不吝点击投票转发,如您有任何疑问或建议，请留言评论。