【抽象代数】Z[sqrt(-5)]里面的理想类
来源:网络收集 点击: 时间:2024-04-13【导读】:
前面,我们找出了Z里面的所有单位。在《代数整数环的可视化》里面,我们用网络画板的迭代功能,画出了虚二次域的代数整数环在复平面上对应的格。这些格的子格,对应着环的理想。本文,我们来寻找这个环的理想类。工具/原料more电脑网络画板方法/步骤1/7分步阅读 2/7
2/7 3/7
3/7 4/7
4/7
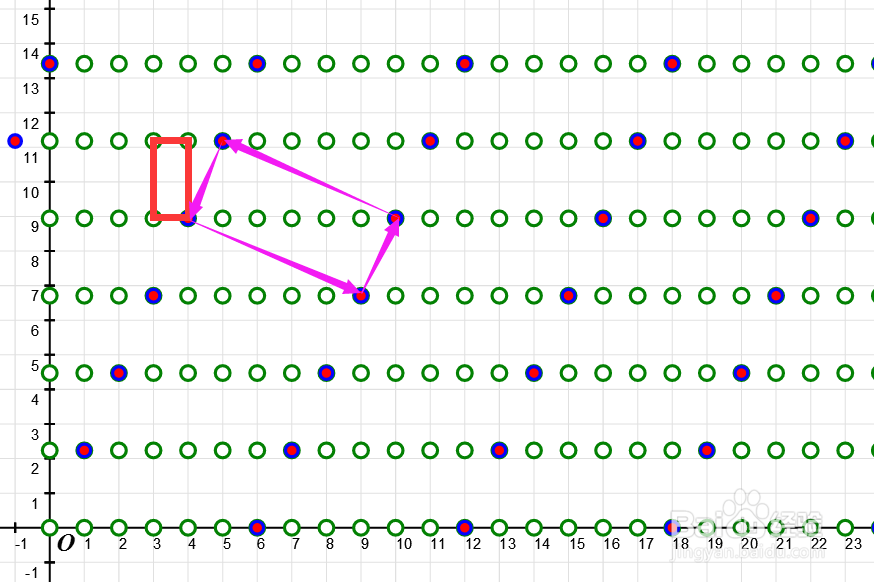 5/7
5/7 6/7
6/7 7/7
7/7 注意事项
注意事项
设δ=sqrt(-5),环R=Z=Z,R在复平面上表现为长方形的格。
 2/7
2/72是R里面的元素,由生成的主理想(2)在在复平面上也表现为长方形,不过更大。
这恰好说明,(2)对应的格是R的子格。
 3/7
3/7主理想(3)对应的格。
 4/7
4/7主理想(1+δ)对应的格。
由此可见,所有的主理想都是相似的。

 5/7
5/7由元素2和1+δ生成的理想(2,1+δ)不是主理想,因为(1+δ)/2不是这个环的单位。
 6/7
6/7理想(2,1+δ)对应的格是某种特定形状的平行四边形。
 7/7
7/7理想(3,1+δ)对应的格某种平行四边形。
请思考:这个平行四边形和上面的平行四边形是否相似?
 注意事项
注意事项你能证明,Z只有两种理想类吗?或者说,图中的格只有两种形状的子格。
求证:(4,1+δ)=(2,1+δ),也就是证明存在整数a、b、c、d,使得a-5b+4c=2且a+b+4d=0。这样有助于绘制(4,1+δ)的格。
版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_505168.html
上一篇:如何对文本框设置文字边距
下一篇:汽车之家账户余额如何进行提现
 订阅
订阅