【Mathematica】双纽线的旋转和验证
来源:网络收集 点击: 时间:2024-05-05【导读】:
之前两篇文章中涉及的中心对称曲线,也是双纽线,只不过参数方程比较怪异。本文,就来证明,这条曲线确实是双纽线。工具/原料more电脑Mathematica方法/步骤1/6分步阅读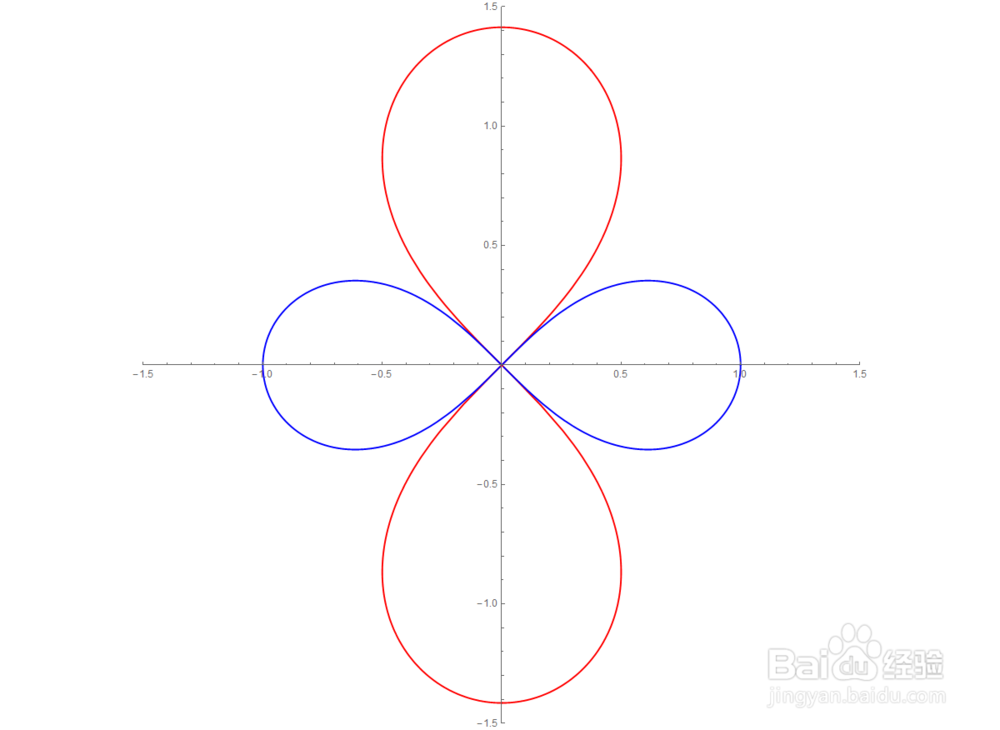 2/6
2/6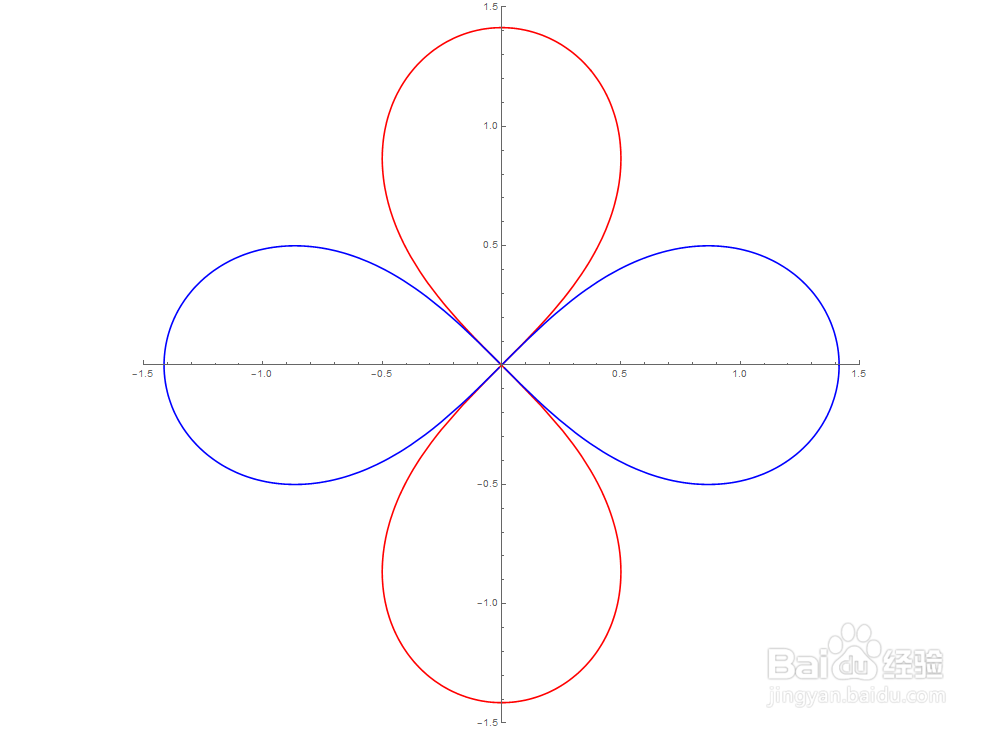 3/6
3/6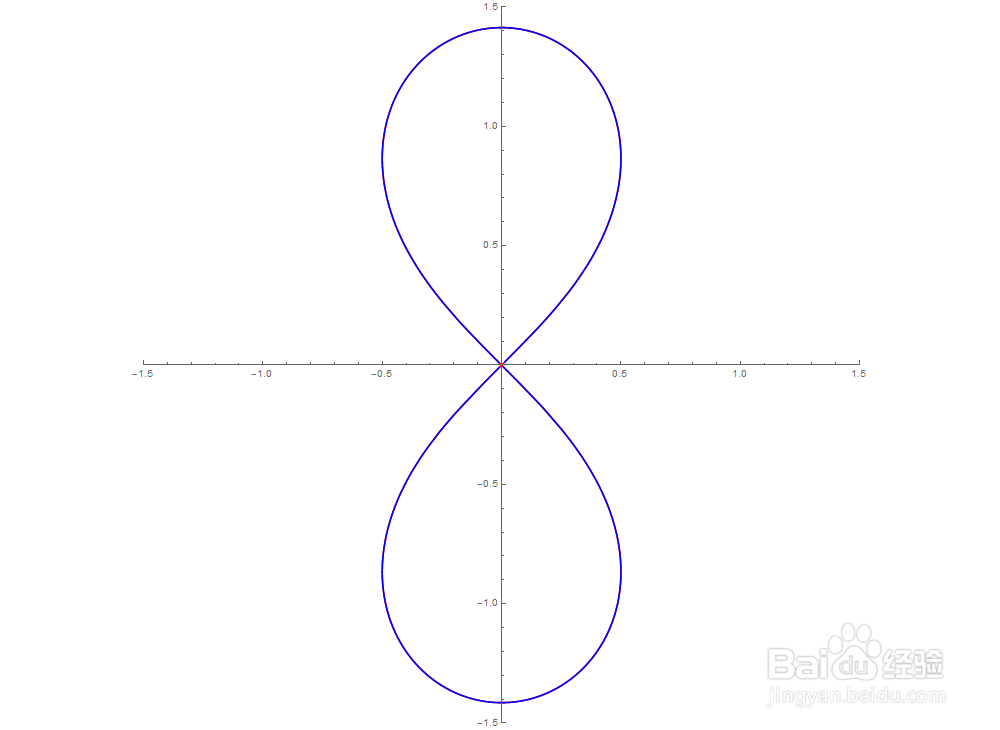 4/6
4/6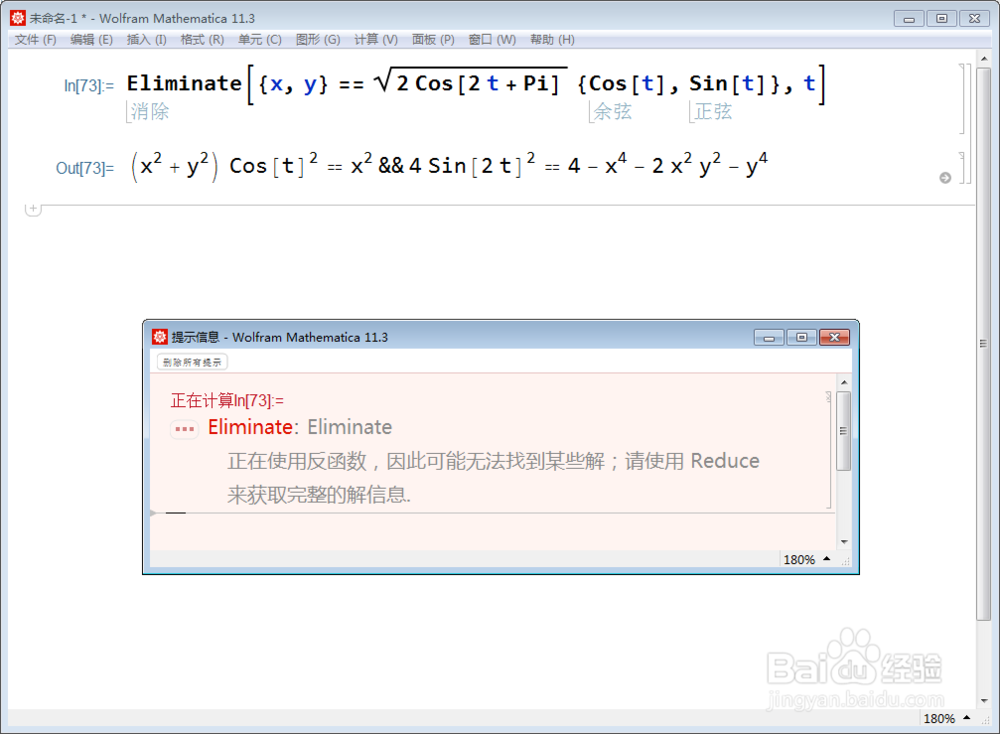 5/6
5/6 6/6
6/6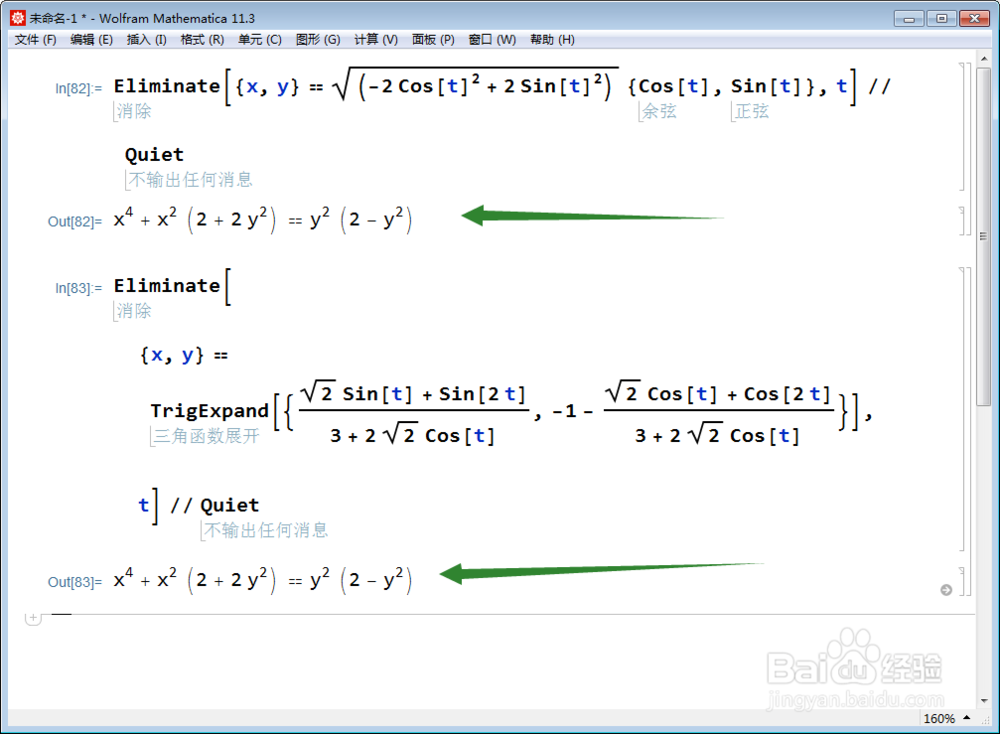
双纽线的极坐标方程是:
ρ=Sqrt]
图中红色曲线的参数方程是:
{(Sqrt Sin + Sin)/(3 + 2 Sqrt Cos),
-1 - (Sqrt Cos + Cos)/(3 + 2 Sqrt Cos)}
本文,就来证明,这两个曲线都是双纽线。
 2/6
2/6把双纽线按比例放大:
ρ=Sqrt]
 3/6
3/6再把双纽线旋转90°:
ρ=Sqrt]
与红色曲线重合了,至少看起来是如此。
 4/6
4/6要想验证这两个曲线完全重合,就需要它们的隐函数方程一样。
双纽线的隐函数方程是,可以通过消去参数来实现,但为什么消不去呢?
 5/6
5/6把三角函数的倍角全部展开,再消参数,就可以成功:
 6/6
6/6把红色曲线也消去参数;
明显,二者的参数方程一样,所以,红色曲线也是双纽线。
把x和y换为-x和-y,方程式不变,表示双纽线是中心对称图形。

版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_682976.html
上一篇:教你怎么做牛尾汤(牛肝菌)
下一篇:小艺输入法剪贴板怎样增大容量
 订阅
订阅