Mathematica 卡方分布
来源:网络收集 点击: 时间:2024-02-18【导读】:
使用Mathematica计算和处理卡方分布和卡分布,以及绘图,变换,产生随机数等操作。工具/原料moreMathematica 11.0方法/步骤1/7分步阅读 2/7
2/7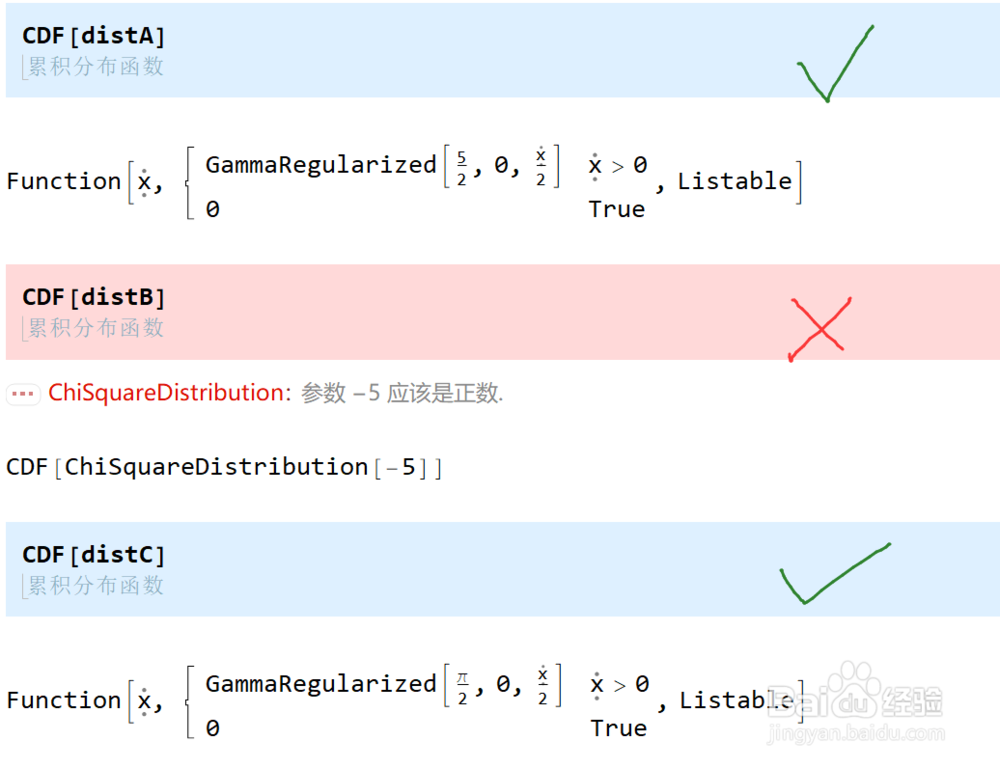 3/7
3/7 4/7
4/7 5/7
5/7 6/7
6/7 7/7
7/7 注意事项
注意事项
首先介绍卡方分布的符号。在Mathematica中,使用:
ChiSquareDistribution
来描述一个指定参数的卡方分布。在描述分布的符号中,参数不论正负都是合法的,尽管用该参数可能无法得到一个分布。
 2/7
2/7使用CDF来求得分布对应的累积分布函数。
卡方分布对于正实数参数都是有意义的。
 3/7
3/7使用PDF以计算一个卡方分布的概率密度。
如图,是参数为n的卡方分布密度表达式。
Gamma就是Γ函数。对于非负整数n,Γ(n+1)=n!
 4/7
4/7如图,分别绘制一个卡方分布的累积分布和概率密度。
图中橘黄色是概率密度。
 5/7
5/7Mean,Variance,Median均可以用于概率分布。
它们分别计算一个分布的平均值,方差和中位数。
如图是卡方分布的结论。
 6/7
6/7卡分布是卡方分布中的随机变量的平方根的概率分布。
变换方法和概率密度如图所示。
 7/7
7/7使用RandomVariate来产生伪随机数。
使用直方图绘制如图。
 注意事项
注意事项CDF求得累计分布函数,假设累计分布是f(x),则f(x)=随机变量小于x的概率之和。
卡方分布和正太分布密切。若X1,X2...Xn是独立同分布的正太分布,则X1^2+X2^2+...+Xn^2是参数为n的卡方分布。
MATHEMATICA概率分布卡方分布概率密度版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_68755.html
上一篇:魅族手机的隐私模式指纹功能怎么打开?
下一篇:微光怎么样关闭展示我的厅
 订阅
订阅