订阅【平面几何】共用内切圆和外接圆三角形的透视
来源：网络收集 点击： 时间：2024-05-10【导读】：
设△ABC的外接圆和内切圆分别是圆U和圆V。D是外接圆上的动点，D到内切圆的两条切线与外接圆交于E和F。请问，什么时候，△DEF和△ABC是透视对应？工具/原料more电脑网络画板第一种情形1/2分步阅读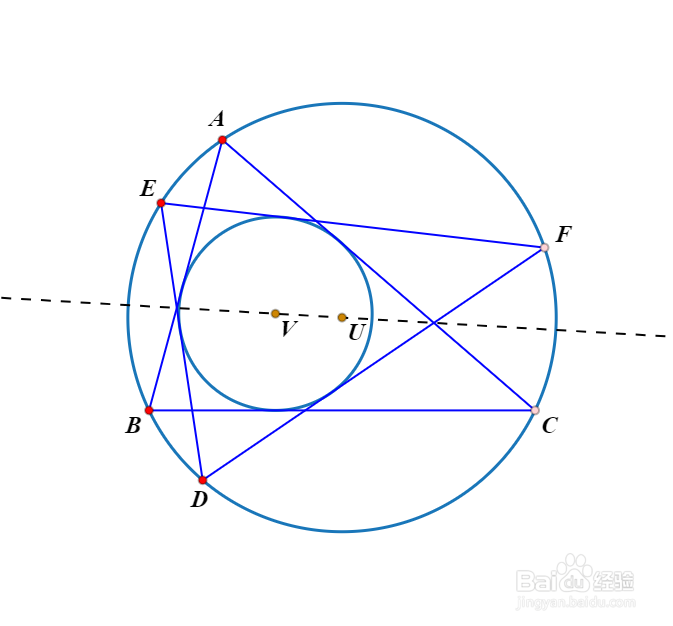
2/2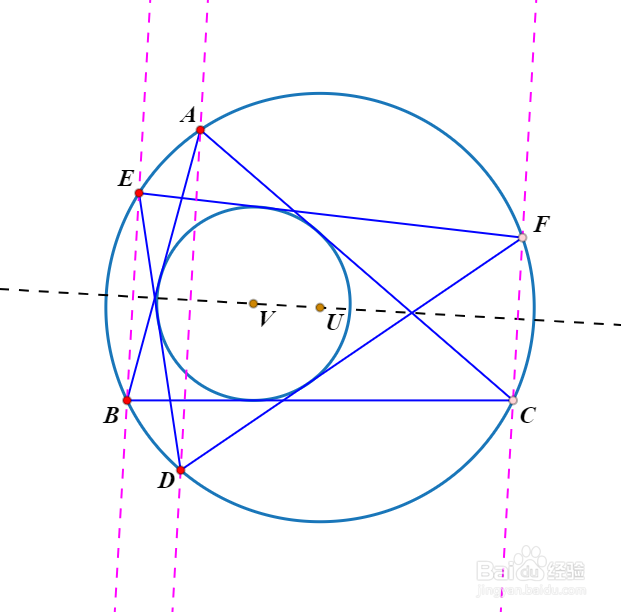
情形二1/2
2/2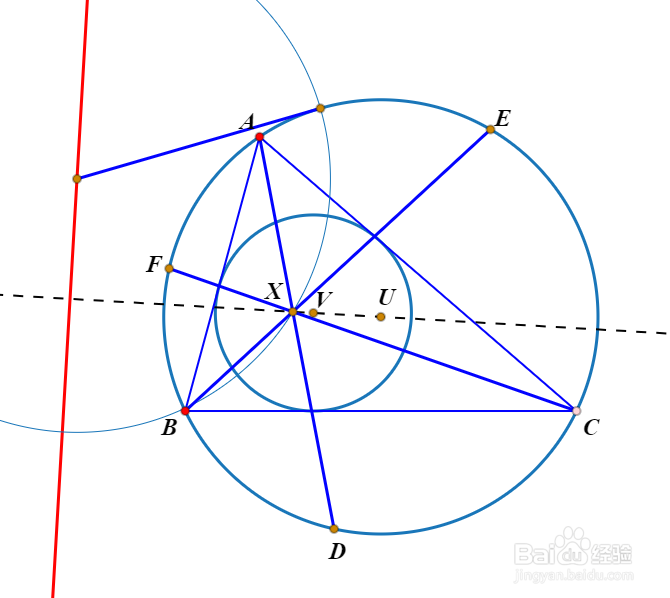
情形三1/2
2/2
注意事项
△DEF和△ABC关于直线UV对称。
2/2此时的透视中心是直线UV的垂线上的无限远点。
情形二1/2△ABC的Gergonne点X作为透视中心。
2/2此时的点X实际上，是由△ABC的外接圆和内切圆产生的共轴圆系的一个极限点。
至于极限点的作图方法，可以参考《怎么构造共轴圆系的极限点？》
情形三1/2由△ABC的外接圆和内切圆产生的共轴圆系的第二个极限点，也可以作为透视中心。
如下图的点Y。
2/2此时的透视三角形DEF，如下图所示。
注意事项实际上，△DEF与△ABC透视，就只有上述三种情形。
版权声明：
1、本文系转载，版权归原作者所有，旨在传递信息，不代表看本站的观点和立场。
2、本站仅提供信息发布平台，不承担相关法律责任。
3、若侵犯您的版权或隐私，请联系本站管理员删除。
4、文章链接：http://www.1haoku.cn/art_730888.html
