本条经验主要介绍多重共线性的处理，将会在其他经验更新多重共线性的理解问题。工具/原料more电脑stata方法/步骤1/6分步阅读

对于多重贡献性的判断依赖的主要是方差膨胀因子，在此处我们来简要介绍一下方差膨胀因子。此处，仅简单的理解方差膨胀因子，就是方差膨胀因子构成了变量估计值方差的一部分，如果方差膨胀因子过大，将会导致解释变量的系数方差增大，将会导致检验难以通过。

观察下面的两个公式,可以很容易地看出这一点。VIF就是方差膨胀因子。

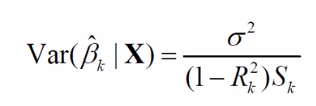
2/6

先对模型进行回归

sysuse auto

gen weight2=weight^2

reg price rep78 weight2 headroom trunk weight length

为什么把函数形式设定成这样可以参考我上一条RESSET的检验

3/6

检验方差膨胀因子

estat vif

见图1，我们发现方差膨胀因子非常之大，说明存在多重共线性

weight 和 weight的平方有很严重的多重共线性

4/6

reg weight2 weight

显然，因为是平方项，回归系数肯定是显著的 R方也是方差大，方差膨胀因子肯定也非常大。

5/6

不过没关系，我们可以对这个问题进行处理，也就是对变量进行标准化，其实衡量的就是去除量纲之后，到均值的距离。

6/6

使用高级的gen明明，生成标准化变量weightsd

egen weightsd=std(weight)

reg price rep78 weightsd2 headroom trunk weightsd length

进行回归，观察weight 发现p值变为了0，效果十分显著。原来是0.437，图2未标准化的回归结果

estat vif

发现VIF降低的十分明显，但仍存在多重共线性（我们认定10一下，多重共线性可以忽略），但是已经下降的十分明显。

注意事项

本条使用于处理放入解释变量平方项的多重共线性问题的解决

有任何关于多重共线性和计量经济学的问题都可以点击下面的疑问给我留言

计量经济学STATA多重共线性