【抽象代数】二阶域的扩展
来源:网络收集 点击: 时间:2024-02-17二阶域里面只有两个元素,0和1。你要想扩展这个域,必须添加里面没有的元素。
你可能会添加一个数字2,但是请注意,在二阶域里面,2=0。二阶域是正整数环塌缩而来的。
你务必添加一个mod2不等于0或1的数字。
大家思考一下,下面四个元素能不能构成一个四阶域?
 2/8
2/8如果往二阶域里面添加2的三次根,情况比较复杂。
下面四个元素不是一个完整的域,因为在四则运算下,不能保持封闭。
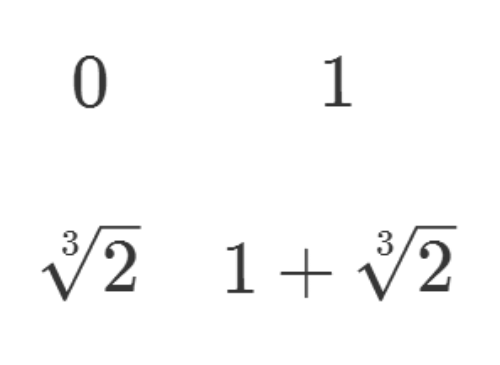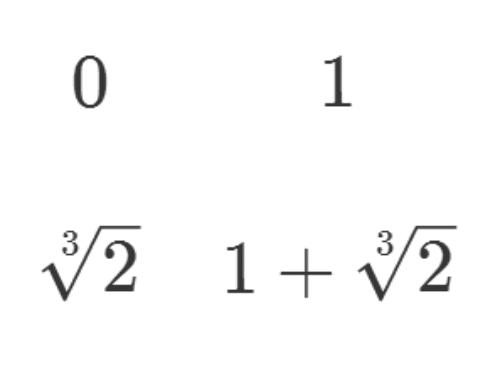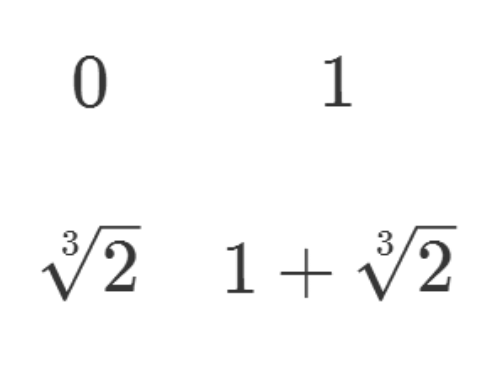
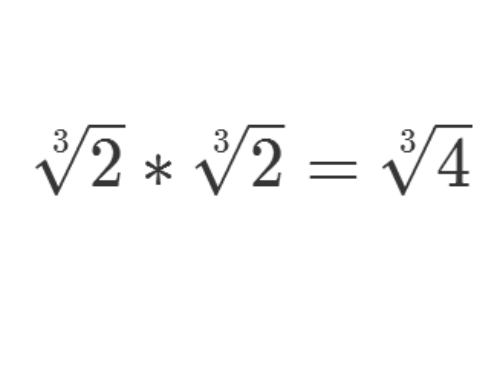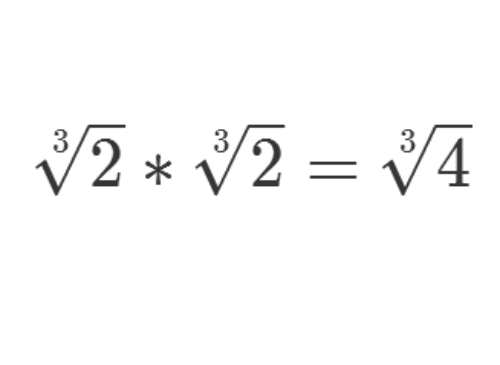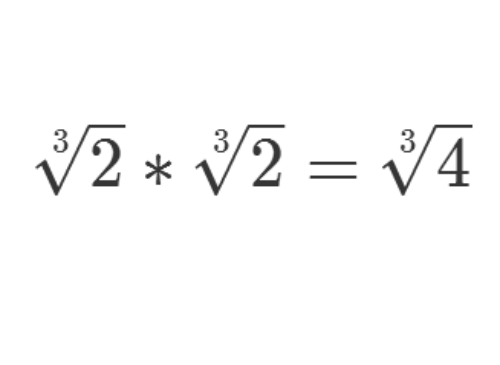 3/8
3/8从已有的元素进行四则运算,直到元素不再增加为止。
这样,可以求出扩展域的所有元素。
设a=2^(1/3),那么,1+a是一个四阶元素。
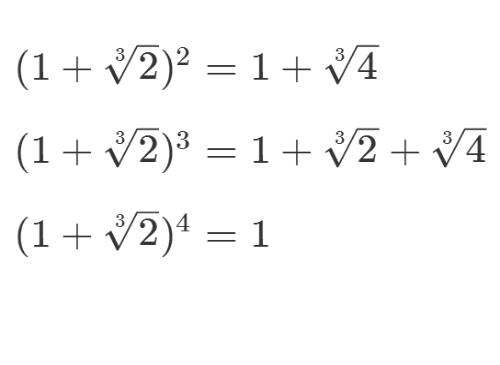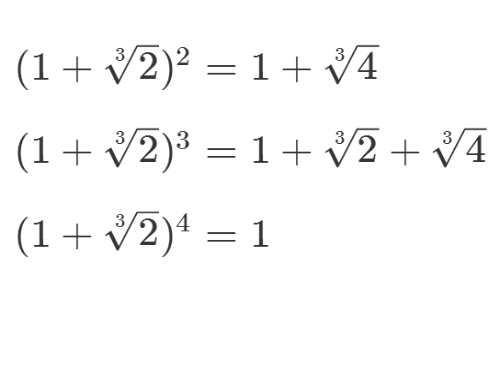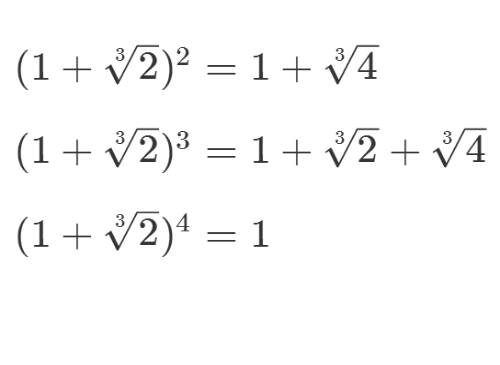 4/8
4/8a本身是几阶元素?
我们发现,在二阶域里面,a的任意正整数次幂,都不会等于1,因此a是零阶元素。这说明这个元素不能用来扩展二阶域。
 5/8
5/8换一个数,a=3^(1/3)。
这样,a是一个3阶元素。
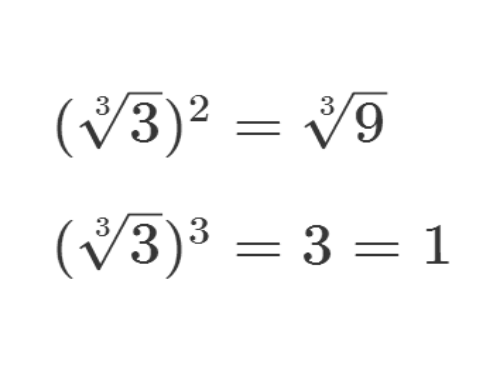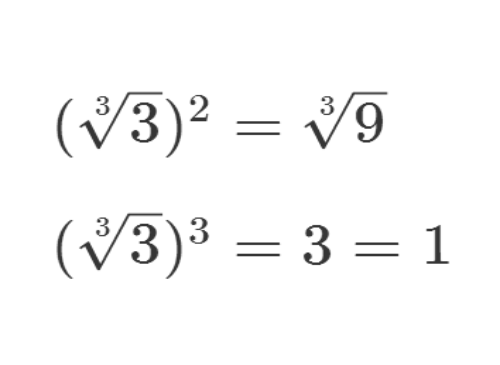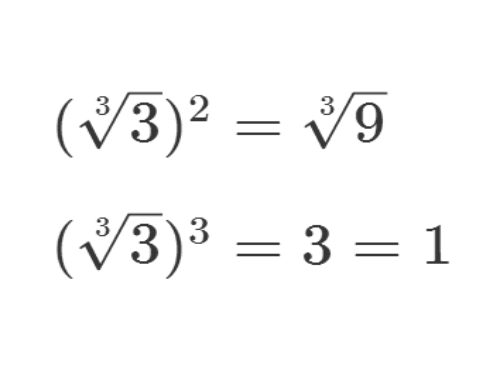 6/8
6/8这样,a的乘法逆就是a^2。
我们再看看b=1+a的乘法逆是否存在。下图中发现,b^4=b,但是,b≠0且b≠1。这是一种矛盾的现象。为什么会如此?
原来,多项式x^3-3在二次域里面不是既约多项式。
 7/8
7/8二阶域唯一的二次既约多项式是:
x^2+x+1
它的根是扩展二阶域为四阶域的唯一出路。假设它的两个根分别是a和b,那么:
ab=1
a+b=-1=1
因为ab=1,所以,a的倒数,或者说a的乘法逆就是b;
因为a+b=1,所以,b=1-a=1+a。
四阶域有四个元素,分别是:0、1、a、b。
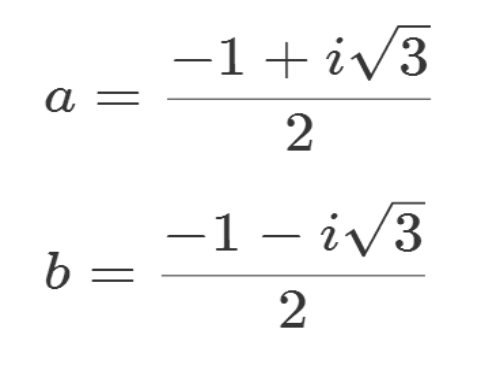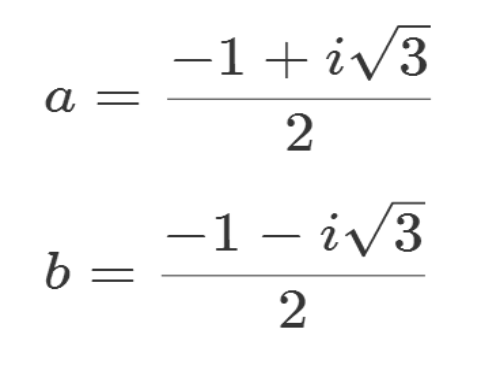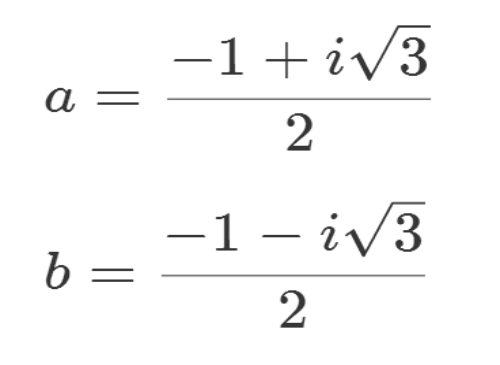 8/8
8/8四阶域还可以视为二阶域的二维向量空间。
这两种写法之间存在一个同构关系:
f((m,n))=m*1+n*a
其中,m和n是二阶域的元素,而1和a则视为基。
 注意事项
注意事项在扩展某个域的时候,务必选择既约多项式的根,否则将难以奏效。
版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_58516.html
 订阅
订阅