正弦函数y=2sin(2x+π/3)的性质归纳
来源:网络收集 点击: 时间:2024-04-30【导读】:
主要内容,本文主要归纳三角函数y=2sin(2x+π/3)的定义域、值域、单调、周期、对称轴、切线等有关性质。工具/原料more导数与函数性质正弦函数性质函数的基本性质1/9分步阅读 2/9
2/9 3/9
3/9 4/9
4/9 5/9
5/9
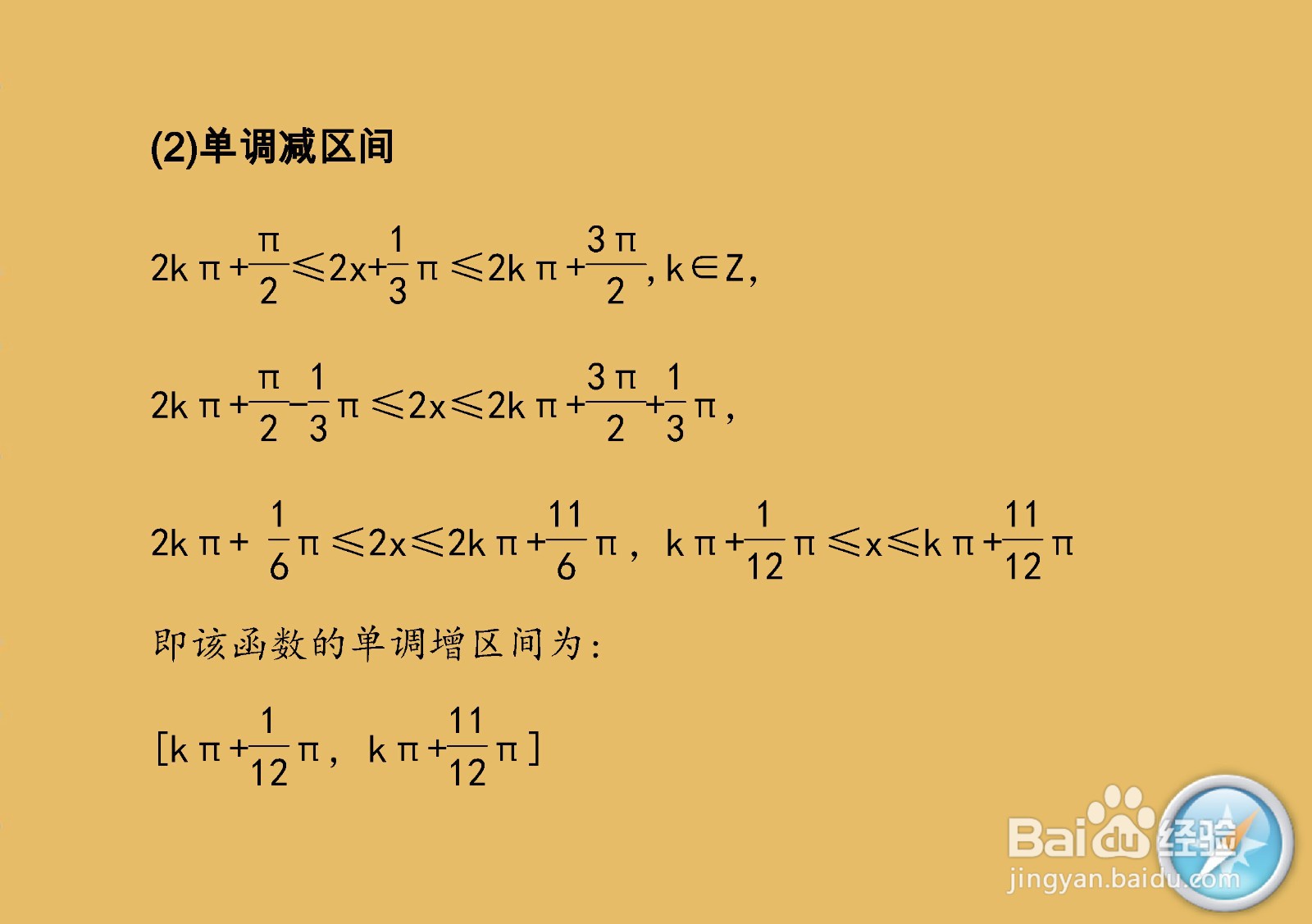 6/9
6/9 7/9
7/9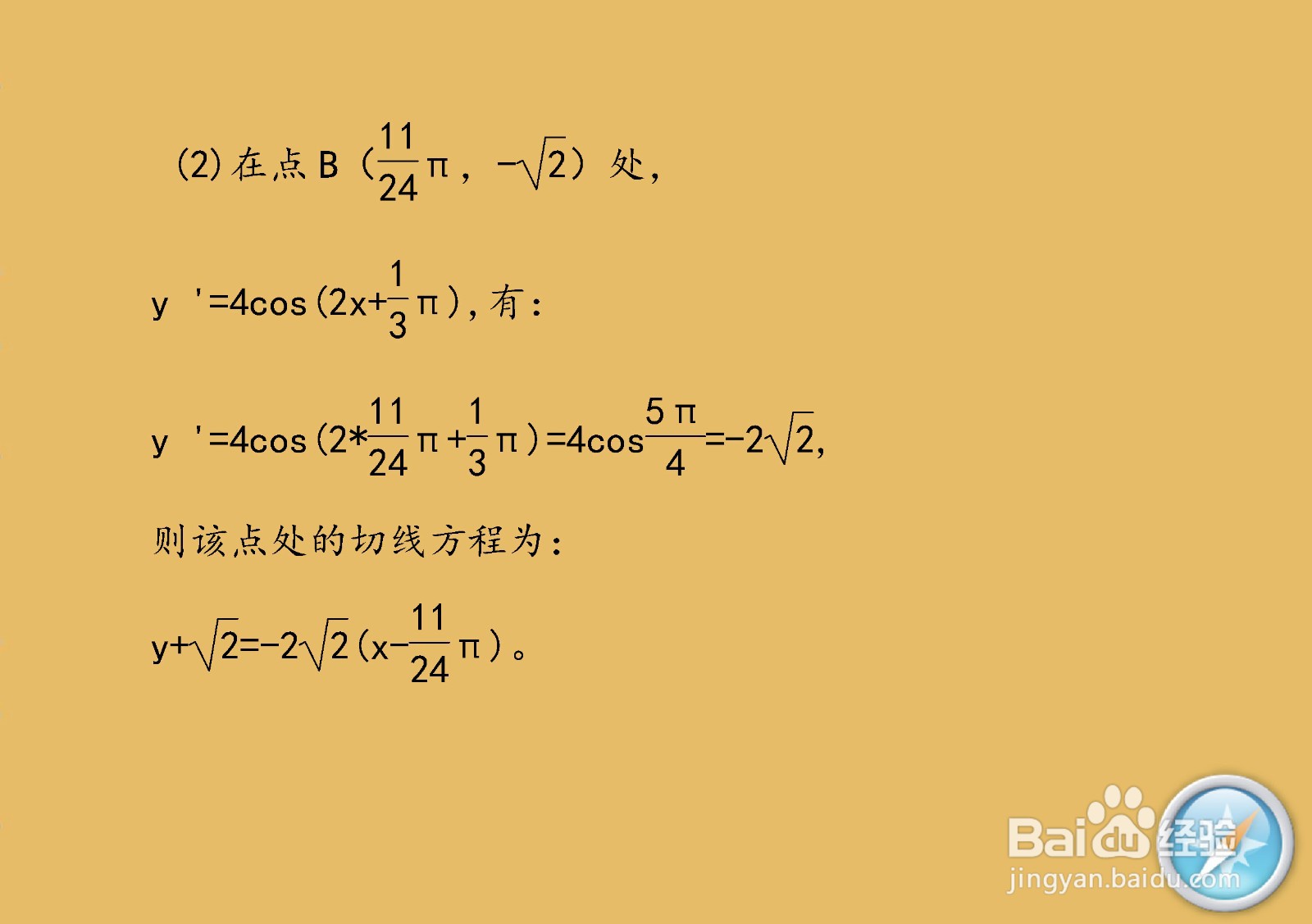 8/9
8/9 9/9
9/9
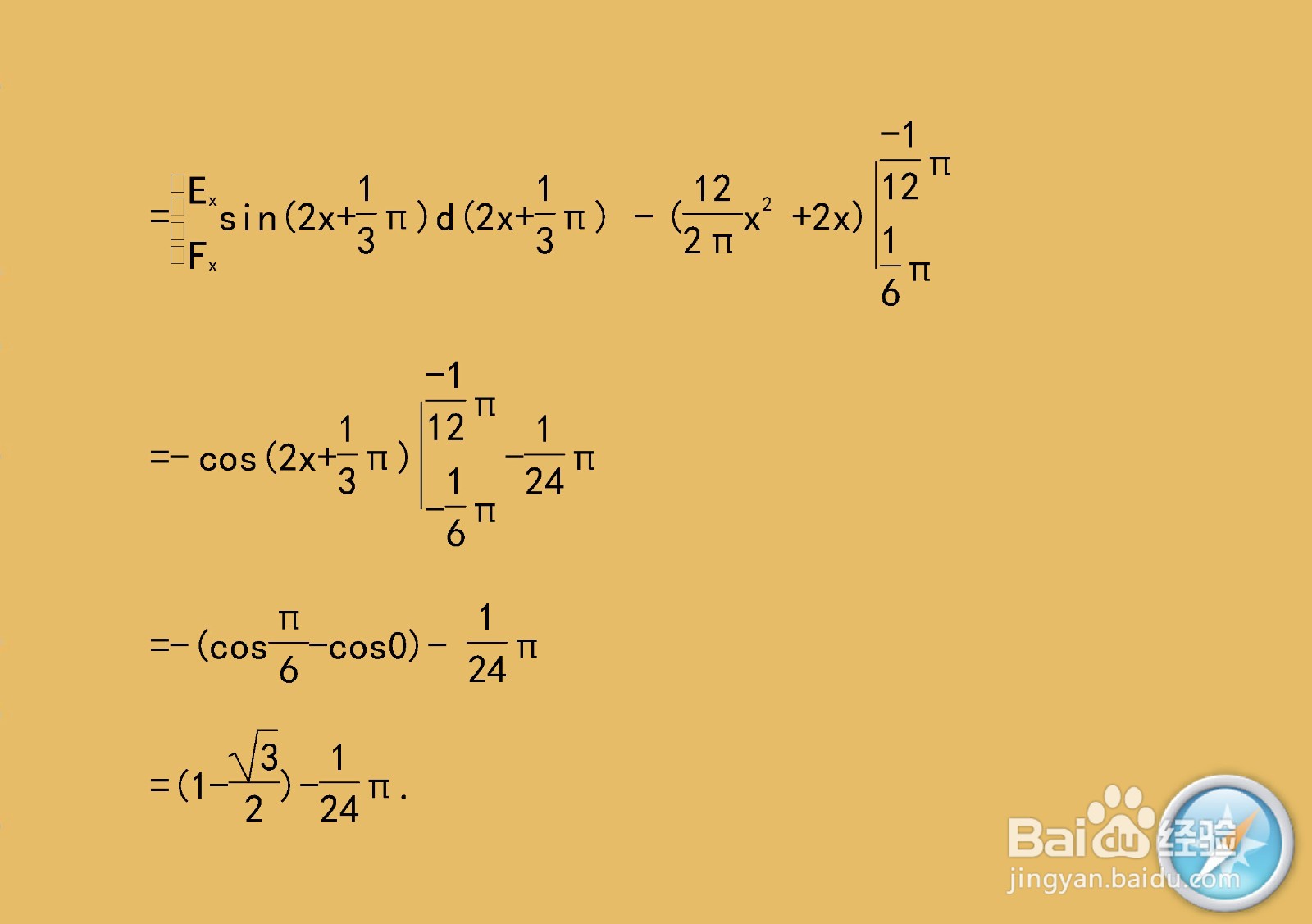 注意事项
注意事项
正弦三角函数的定义域、值域和最小正周期等基本性质如下。
 2/9
2/9根据三角函数的性质,求出正弦三角函数的对称轴:
 3/9
3/9正弦三角函数对称中心是与x轴上的交点,即可得到函数的对称中心。
 4/9
4/9由正弦函数的导数公式y=sinx,y=cosx,即可求解该正弦函数的一阶导数、二阶导数,并和推解其高阶导数。
 5/9
5/9以基本正弦函数y=sinx的单调增区间和减区间,即可推导求出正弦复合函数的单调增区间和减区间。

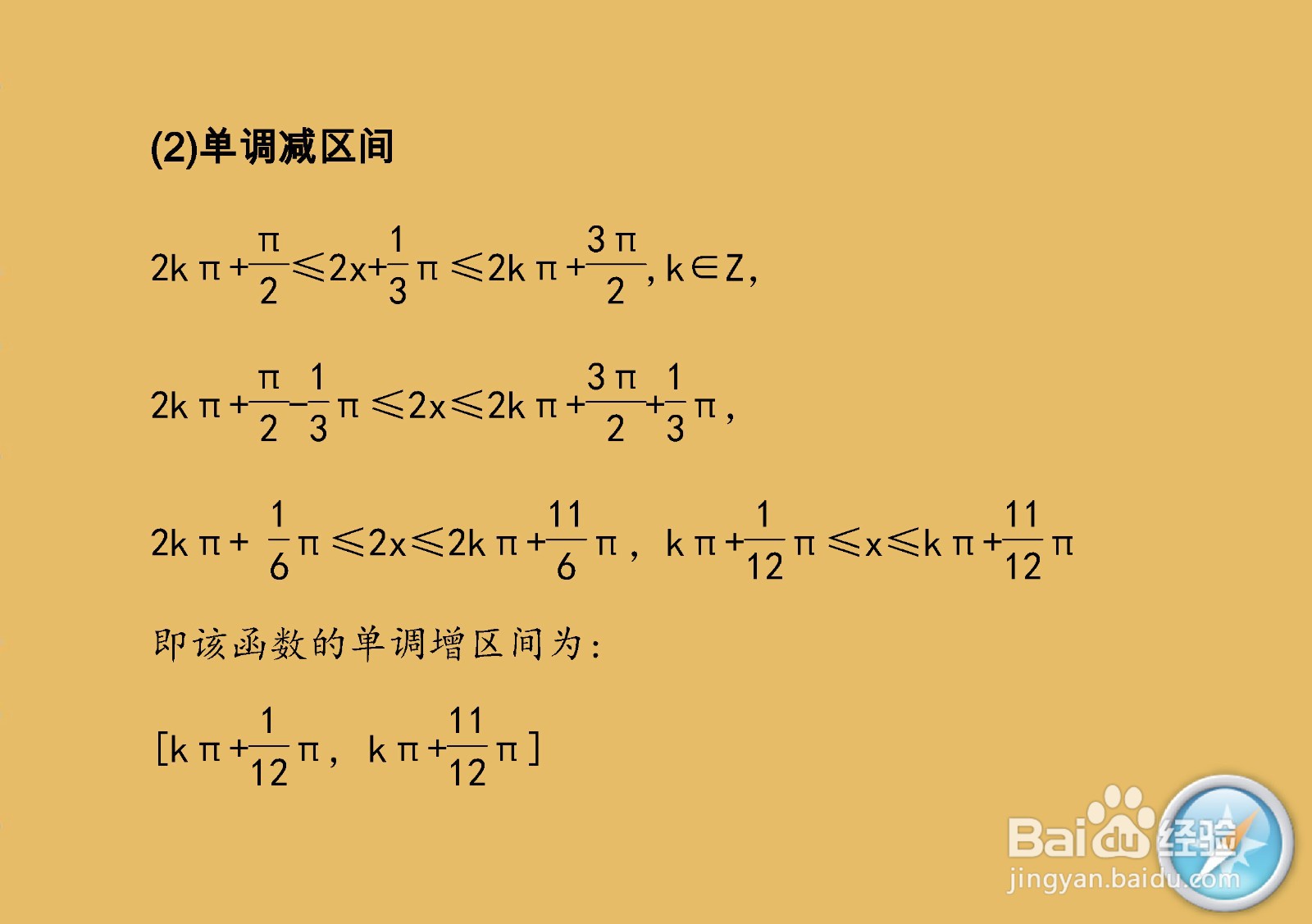 6/9
6/9用导数知识,求解函数在点A(-π/12,1)处切线的主要过程和步骤。
 7/9
7/9根据导数的几何意义,求解函数在点B(11π/24,-√2)处切线的主要过程和步骤.
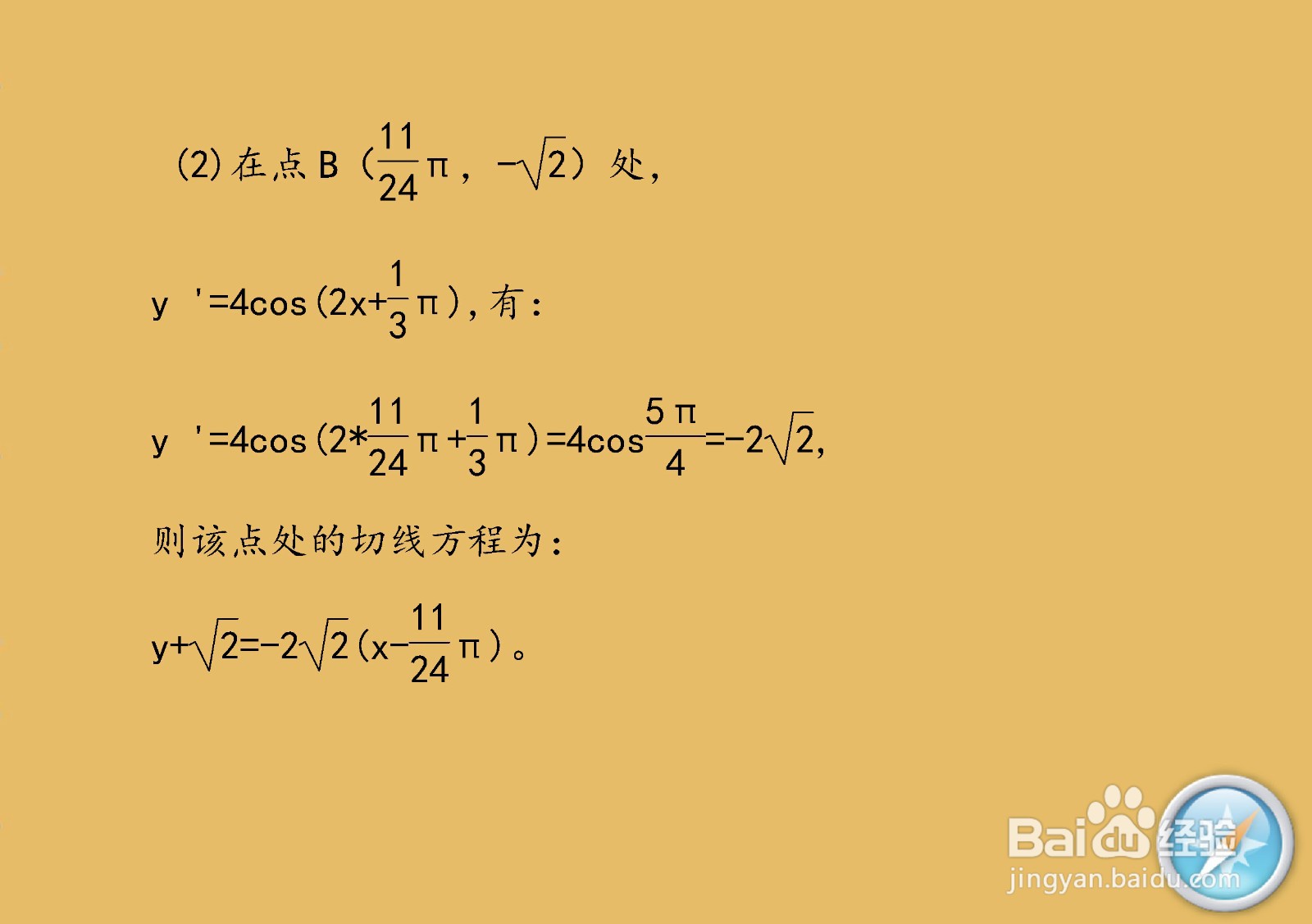 8/9
8/9根据定积分有关知识,计算该正弦函数在半个周期的与坐标轴围成的区域的面积,主要过程如下:
 9/9
9/9举例介绍计算直线与正弦函数围成的区域面积的主要方法与步骤。

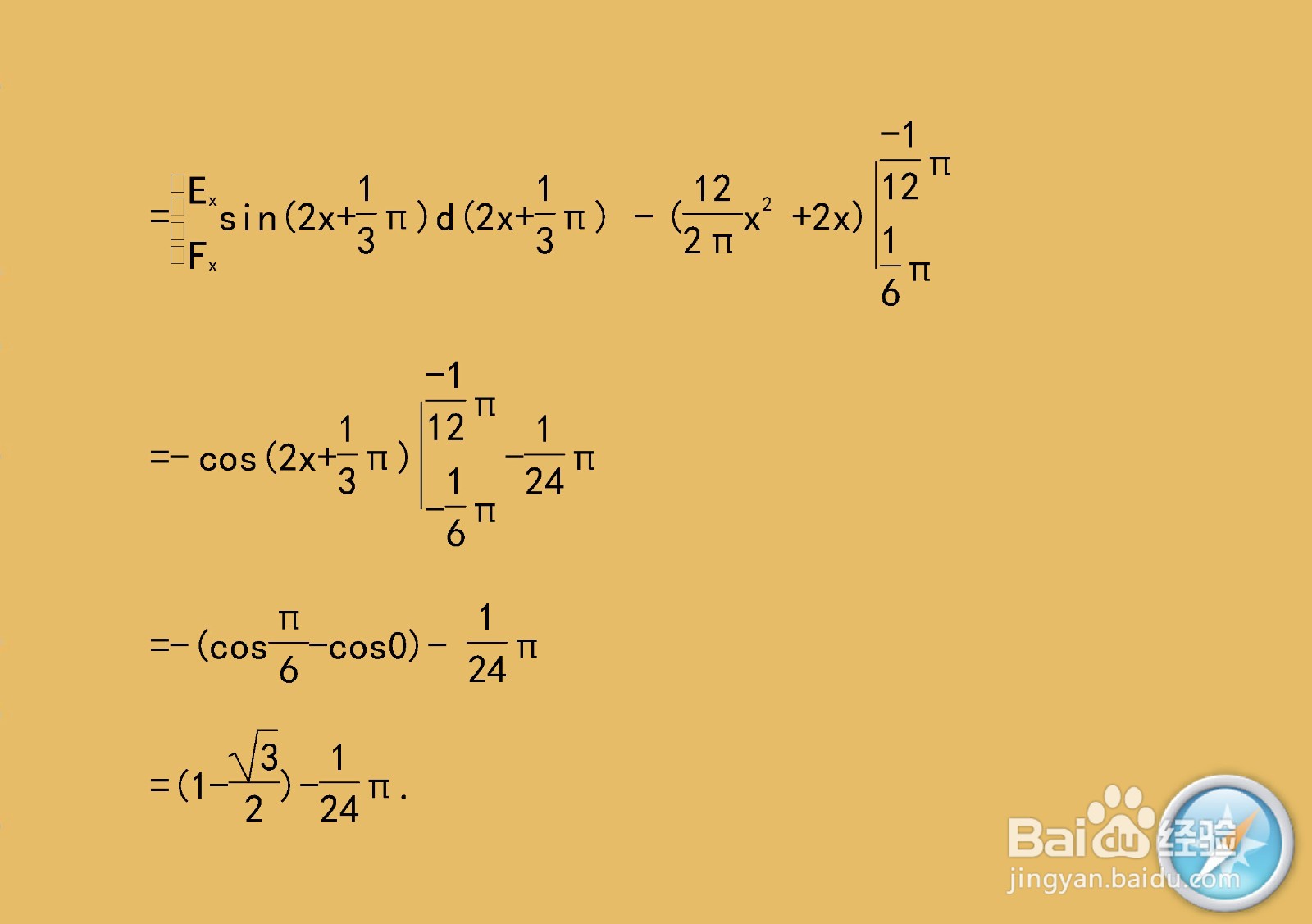 注意事项
注意事项定积分可用于求解不规则区域的面积
三角函数导数性质版权声明:
1、本文系转载,版权归原作者所有,旨在传递信息,不代表看本站的观点和立场。
2、本站仅提供信息发布平台,不承担相关法律责任。
3、若侵犯您的版权或隐私,请联系本站管理员删除。
4、文章链接:http://www.1haoku.cn/art_631189.html
上一篇:陌陌极速版如何查看已加入的粉丝团
下一篇:怎样制作开机动画
 订阅
订阅